Software Key Tutorial
.
In computer science, queues are essential data structures (DS) that follow the First-In-First-Out (FIFO) rule. It resembles a line of customers waiting for service since things are added to the back and removed from the front of the queue. There are various queue kinds, each serving a different purpose.
In this tutorial, let's learn in detail about the types of queues, types of queues in DS, and types of queues with examples alongside certain aspects of operations of queues in data structure and circular queue in data structure.
A queue is a fundamental data structure that adheres to the First-In-First-Out (FIFO) principle in computer science and information technology. Elements are added to a queue from the back (enqueue) and taken out from the front (dequeue). This behavior resembles a line in real life, such as one at a café or ticket window.
A queue is a linear data structure used in computer programming that adheres to the First-In-First-Out (FIFO) rule. It is an organized group of elements, with new elements going to the back (rear) and old ones going to the front (front) of the queue. To simulate a real-world queue, such as people waiting in line, the element that has been in the queue the longest is the first one to be taken out.
When the sequence of processing or managing data is important, queues are frequently employed to handle the data. They have several uses in computer programming, such as managing resources, scheduling tasks, using breadth-first search methods, mimicking actual systems, dealing with asynchronous processes, and more.
Different types of queues have specific use cases and advantages. For example, simple queues are often used in scenarios where elements need to be processed in the order they arrive. Circular queues are useful in scenarios where memory efficiency is important and the queue might wrap around. Priority queues are great for managing tasks with different levels of urgency. Double-ended queues are versatile and can handle both FIFO and LIFO requirements.
Let us learn more about these queues:
A simple queue, also known as a linear queue, is a basic form of a queue where elements are added at the rear (enqueue) and removed from the front (dequeue). It follows the First-In-First-Out (FIFO) principle, meaning that the first element added to the queue is the first one to be removed.
A circular queue is an extension of the simple queue where the rear and front are connected in a circular manner. When the rear reaches the end of the queue, it wraps around to the beginning. This allows for more efficient use of memory compared to a simple queue, where the queue might become empty or full prematurely.
A priority queue is a type of queue where each element has an associated priority. Elements are removed from the queue based on their priority, not their arrival time. Higher-priority elements are dequeued before lower-priority elements. Priority queues are commonly implemented using binary heaps or other heap data structures.
A double-ended queue, often abbreviated as "deque," is a versatile queue that allows elements to be added or removed from both the front and the rear. It supports both FIFO and LIFO (Last-In-First-Out) operations, making it useful for various scenarios. Deques can be thought of as a combination of a stack and a queue.
Here are the primary operations performed on a queue:
Enqueue (Insertion): Enqueue operation is used to add an element to the rear (end) of the queue. The newly added element becomes the last one to be removed.
Dequeue (Deletion): Dequeue operation removes the element from the front (beginning) of the queue. The element that has been in the queue the longest is dequeued.
Peek (Front): Peek operation retrieves the element at the front of the queue without removing it. This allows you to see which element is next in line to be dequeued.
IsEmpty: IsEmpty operation checks whether the queue is empty or not. It returns a Boolean value indicating whether there are any elements in the queue.
Size: Size operation returns the number of elements currently present in the queue.
Here is an example of how you might perform these operations using Python's built-in list as a simple queue:
queue = [] # Enqueue queue.append(1) queue.append(2) queue.append(3) # Dequeue dequeued_item = queue.pop(0) # Remove and return the first element # Peek (Front) front_item = queue[0] # IsEmpty is_empty = len(queue) == 0 # Size queue_size = len(queue)
In this example, elements are added to the queue using the append() method, and the pop(0) method is used to remove elements from the front. The first element in the queue can be accessed with queue[0], and the size of the queue is determined using the len(queue) function.
For more efficient queue implementations, we can consider using Python's collections.deque (double-ended queue) or, for specialized use cases, the queue.Queue class from the queue module. These implementations provide better performance for enqueue and dequeue operations.
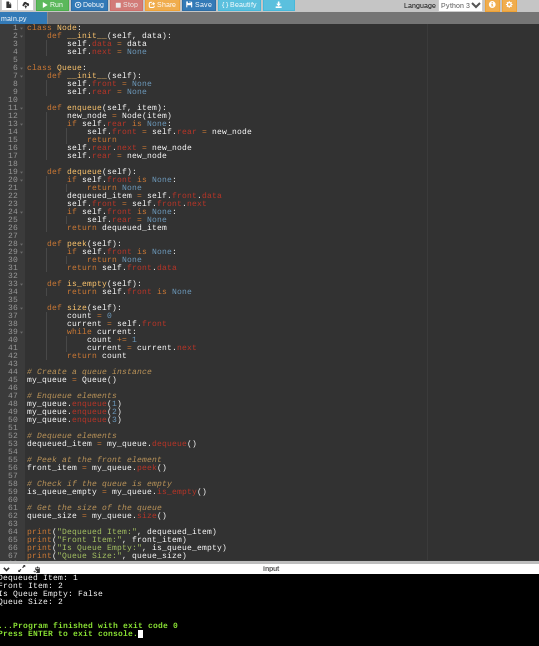
Here is an example of implementing a basic queue in Python using the collections.deque class, which provides efficient enqueue and dequeue operations:
from collections import deque
class Queue:
def __init__(self):
self.queue = deque()
def enqueue(self, item):
self.queue.append(item)
def dequeue(self):
if self.is_empty():
return None
return self.queue.popleft()
def peek(self):
if self.is_empty():
return None
return self.queue[0]
def is_empty(self):
return len(self.queue) == 0
def size(self):
return len(self.queue)
# Create a queue instance
my_queue = Queue()
# Enqueue elements
my_queue.enqueue(1)
my_queue.enqueue(2)
my_queue.enqueue(3)
# Dequeue elements
dequeued_item = my_queue.dequeue()
# Peek at the front element
front_item = my_queue.peek()
# Check if the queue is empty
is_queue_empty = my_queue.is_empty()
# Get the size of the queue
queue_size = my_queue.size()
print("Dequeued Item:", dequeued_item)
print("Front Item:", front_item)
print("Is Queue Empty:", is_queue_empty)
print("Queue Size:", queue_size)In this example, the Queue class wraps a deque instance and provides methods for the common queue operations. It demonstrates how to enqueue elements, dequeue elements, peek at the front element, check if the queue is empty, and get the size of the queue. Remember to import deque from the collections module.
There are several ways to implement a queue in programming. Each implementation has its own advantages and trade-offs in terms of efficiency, memory usage, and ease of use.
Here are some common ways to implement a queue:
You can use built-in lists or arrays to implement a queue. In this approach, you can use the append() method to enqueue elements and the pop(0) method to dequeue elements. However, this approach can be inefficient for dequeuing because pop(0) has a time complexity of O(n) since it requires shifting elements. If you're using a list, consider using collections.deque instead, as it provides more efficient enqueue and dequeue operations.
The collections module in Python provides the deque class, which is a double-ended queue. It's a great choice for implementing queues as it offers fast enqueue and dequeue operations with O(1) time complexity.
Linked lists can be used to implement a queue. In this approach, each element in the queue is a node in a linked list. Enqueueing involves adding a new node to the end of the list, and dequeueing involves removing the first node from the list. Linked lists can provide efficient enqueue and dequeue operations if you maintain references to both the head and tail nodes.
The queue module in Python provides the Queue class, which implements a thread-safe queue. It's useful when you're working with multiple threads and need to ensure safe access to the queue. The Queue class uses collections.deque internally.
This approach uses an array and two pointers, one pointing to the front and another pointing to the rear of the queue. Enqueueing involves moving the rear pointer and adding an element, while dequeueing involves moving the front pointer and removing an element. When the front pointer catches up to the rear pointer, the queue is empty.
You can use two stacks to implement a queue. One stack is used for enqueueing and the other for dequeueing. To dequeue, you can pop all elements from the enqueue stack and push them onto the dequeue stack, effectively reversing the order. This approach can be less efficient than others but is a good exercise in understanding data structures.
Here is an example of using a linked list to implement a queue:
In this example, the Queue class uses a linked list to manage the elements. The Node class represents each element with its data and a reference to the next node. The Queue class maintains two pointers, front and rear, which point to the first and last nodes respectively.
Enqueueing involves adding a new node to the rear, and dequeueing involves removing the node from the front. This implementation provides efficient enqueue and dequeue operations with a time complexity of O(1).
Like every other data structure, queues have their own set of problems and factors that programmers should be aware of while utilizing them. Here are a few typical problems with lines:
Queue Overflow: In many implementations, with a fixed queue size, and added elements without removal, the queue could fill up and overflow.
Queue Underflow: Dequeuing elements from an empty queue may lead to a queue underflow, which could lead to errors.
Synchronization Issues: Using queues to communicate between threads in concurrent or multi-threaded programming might cause synchronization problems.
Priority Inversion: A priority inversion can happen in a priority queue where the elements have various priorities if a low-priority activity holds up the queue and delays the execution of high-priority activities.
Memory Management: When linked lists are used to implement queues, there may be extra costs due to memory allocation and deallocation for each node.
Time Complexity: Depending on the implementation, queue operations might have varying levels of temporal complexity. For instance, because items may need to be moved, linear queues built with arrays may have O(n) time complexity for enqueue and dequeue operations. By reaching time complexity for certain operations, circular queues can get around this restriction.
Inefficient Queue Implementations: Dequeuing items from the front in some queue implementations can be a costly operation, especially when linked lists are involved because it necessitates traversing the list. Dequeuing occasionally turns into a bottleneck.
Limited Dynamic Sizing: It may not be possible to dynamically resize the queue for some queue implementations since they have fixed sizes. This restriction can be a problem when the queue size needs to change according to usage.
In conclusion, queues, which follow the First-In-First-Out (FIFO) principle, are essential data structures in computer programming. They offer an organized and effective method of managing data, enabling easy processing and handling of components. Developers can select the most appropriate solution for their unique requirements thanks to the several queue types that cater to various scenarios and requirements.
You can check out the various programs upGrad has to offer to find out more about different data structures such as queues.
1. Which type of queue is best?
The application context and specific requirements determine the "best" queue type. A circular queue is frequently a wise choice for general-purpose applications since it effectively utilizes space and offers constant-time enqueue and dequeue operations. To ensure effective handling of high-priority components, a priority queue is better appropriate for applications with priority-based processing needs. The use case and performance factors in the end determine which queue type is optimal.
2. Where is the queue mostly used?
Applications in computer science and software engineering frequently use queues. They are frequently used in network packet routing, task scheduling, print job management, message processing systems, and asynchronous event handling. In multi-threaded and concurrent programming environments, queues are also essential because they help with data synchronization and thread communication.
3. Which is the highest priority in the queue?
The element with the highest priority in a priority queue will be the one that is dequeued first. Based on a certain set of criteria or a comparison function that was assigned to the elements during insertion, the priority is decided. The element with the highest priority is processed or handled first since it is given priority over all other elements.
Leave a Reply
Your email address will not be published. Required fields are marked *