Software Key Tutorial
.
The realm of data structures and algorithms contains a plethora of fascinating concepts, one of which is the left view of binary tree. The concept may appear confusing initially, but once understood, it becomes a vital tool for overcoming challenges on competitive programming platforms. This article will shed light on the subject by looking at several approaches, such as recursion, iteration, and language-specific implementations in Java, C++, and Python.
Before diving into the left view, it's essential to understand the fundamental concept of binary trees. A binary tree is a tree-type non-linear data structure with a maximum of two children for each parent. In a binary tree, each node has, at most, two children, typically referred to as the left child and the right child.
The left view of a binary tree refers to the set of nodes visible when the tree is observed from its left side. Consider that you are standing on the left side of the tree, and the tree itself obstructs the view. The nodes you can see make up the left view of the tree. This view can provide unique insights into the tree's structure, making it an invaluable asset in various programming and data analysis tasks.
Recursion is one of the most frequently used methods to print the left view of a binary tree. The logic is straightforward: print the first node at each level of the binary tree.
Approach 1: Using Recursion
The recursive method depends on pre-order traversal, where we process the root, then the left child, and finally the right child. We also pass a level variable in the function to track which level we're currently on. If the current level is higher than our maximum reached level, we print the node since this is the first node of this level observed from the left side.
Implementation
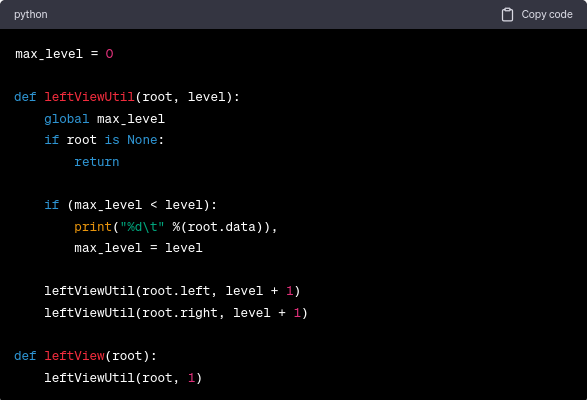
To illustrate the recursive method, let's look at its implementation in the left view of binary tree Python:
This Python code gives the output `1 2 4`, representing the nodes visible from the left side.
Explanation:
Using a depth-first search (DFS) traversal, this Python code computes the left view of a binary tree. It first initializes a global variable named'max_level' to keep track of the utmost tree depth traversed throughout the traversal. The primary function, 'leftViewUtil', is a recursive function that accepts a node and its tree level. It determines if the current node's level is greater than'max_level'. If so, the code outputs the node's data and modifies the'max_level' variable. The function is then called recursively for the left and then the right offspring of the current node, with the level incrementing each time. The 'leftView' function initiates the recursive process by invoking 'leftViewUtil' with the root of the tree and the initial level of 1 as arguments. Therefore, it guarantees that the leftmost node of each level is encountered and printed before any other nodes on the same level.
1. Initialization: The initial value of the global variable'max_level' is 0. This variable tracks the utmost depth level reached during the traversal.
2. The leftViewUtil function: This recursive function performs the bulk of the effort. It requires two parameters: the current node ('root') and depth level ('level').
3. Base Case: If the 'root' node is 'None', which indicates that we have reached the child of a leaf node or that the tree is empty, the function returns without conducting any operations.
4. Check Level: For a non-null node, we determine if the present 'level' exceeds'max_level'. As we traverse the tree from left to right, this condition will be true for the leftmost node of each level.
5. Print Node and Update max_level: If the current level is greater than'max_level', it indicates that we have reached a previously unexplored level of the tree and that the node is the leftmost node on that level. Therefore, we output the node's information and update'max_level' to the present level.
6. Recursive Calls: We make recursive calls for the left child and then the right child of the current node while the level is incremented by 1. To ensure that we encounter the leftmost node of each level before any other nodes at the same level, we visit the left child before the right child.
7. Left View Function: This function initiates the recursive process by invoking 'leftViewUtil' with the root of the tree and 1 as the initial level.
The code will output the left view of the binary tree if these steps are followed.
The level order traversal, or Breadth-First Search (BFS), is another approach to finding the left view of a binary tree.
Approach 2: Using Queue()
In this method, we use a queue data structure. The queue helps us traverse level-by-level from top to bottom and from left to right at each level. We print the first node at each level, which is the node visible from the left side.
Implementation
Here is a simple left view of binary tree C++ code snippet showing the implementation of this approach:
The output of this C++ code is `1 2 4`, which matches the left view of the binary tree.
Explanation:
The function returns if the root is 'NUll', indicating the tree is empty.
Next, a queue named 'q' is created, and the root node is added.
The 'while' loop continues until the queue becomes clear.
Within this iteration, the current queue size 'n' is computed. This dimension indicates the number of nodes at the current tree level.
A nested 'for' loop is utilized to traverse all nodes on the current level. For each vertex:
- It is withdrawn from the front of the queue and stored in the variable 'temp'.
- If the loop index 'i' is 1, indicating that the node is the first on the current level, its data is printed. This phase allows us to print the left view, as it prints the first node encountered on each level.
- If 'temp' has a left child, the left child is appended to the end of the queue.
- If 'temp' has the right child, it is also appended to the queue's end.
The process is repeated until the queue is emptied, ensuring that each level of the binary tree is visited and the leftmost node at each level is printed.
This code essentially employs a queue to perform a level-order traversal and prints the first node encountered at each level, resulting in the left view of the binary tree.
Let's examine an example to better understand these concepts. Given a binary tree:
The left view of this binary tree would be 10, 20, 40.
Different programming languages have unique syntax and capabilities. Therefore, it is essential to understand how to implement these concepts in various languages.
Left View in Java
In Java, we can implement the left view using a similar approach to the Python version. Here's how:
The output of this Java code would be `10 20 40`.
Left View in C/ C++
For C++, we can use either recursion or level order traversal (queue) approach:
This C++ code will output `10 20 40`, which matches the left view of the binary tree.
Hashing can be used to print the left view of a binary tree. The approach here is to assign a 'horizontal distance' to each node. We initialize a variable 'max_level' with 0, and as we traverse the tree, we compute the 'hd' value for each node and compare it with the 'max_level'. If 'hd' is more, then we print the node's data and update 'max_level' with 'hd'.
The output of this Python code would be `10 20 40`.
The most significant benefit is simplicity. Recursion to find the left view uses the base, left toddler, and right baby, replicating the tree structure.
Due to its top-down approach, recursion manages tree structures intuitively.
Less Code: Recursive solutions need fewer lines of code, making them easier to develop and less error-prone.
Recursive data structure: The binary tree is defined in terms of itself. A binary tree has two wings, each a binary tree.
The right view of a binary tree is the set of nodes visible from the right side of the tree. Essentially, if you envision standing on the right side of the tree and looking towards the root, the visible nodes constitute the correct view of the binary tree.
Following are the principal distinctions between the right and left views of a binary tree:
- Nodes in View: The rightmost node of each level is considered for the right view. In contrast, the leftmost node of each level is considered for the left view.
- Traversal Preference: When calculating the right view using depth-first search (DFS), the right subtree is typically given precedence over the left. When determining the left view using DFS, however, we prioritize the left subtree.
- Output Order: If a binary tree is precisely balanced, the left view will display the nodes in the order they would be visited during a preorder traversal (while ignoring the right child nodes). In contrast, the right view would return the nodes in the order they would be visited in a reverse post-order traversal (while disregarding the left progeny nodes).
- Mirrored Views: The right view of the original tree is identical to the left view of the mirrored tree, and vice versa.
Despite these differences, the left view and right view share similar implementation strategies, whether recursion, level order traversal, or hashing are employed. Therefore, comprehension of one can significantly facilitate comprehension of the other.
Binary trees are essential for record control and business enterprise in computing. They are vital additives to laptop technological know-how and software engineering. Gaining a complete understanding of numerous views on a binary tree, especially the left view, can improve our capacity to remedy statistics structure-related troubles efficiently.
Binary trees have several applications, including database management, web technology hierarchy creation, and the development of effective machine learning algorithms. Learning to use tree structures effectively and understanding their attributes can greatly improve your problem-solving ability.
Enforcing the left view of the binary tree in unique programming languages using strategies that include recursion, iteration, and level order traversal can enhance your information and make you a flexible programmer. In contemporary records, possessing these skills surely gives several advantages.
1. What is the time complexity of the level order traversal method to print the left view of a binary tree?
The time complexity of the level order traversal method is O(n), where n is the range of nodes inside the tree. This is because every node is processed most effectively using this method.
2. What is the top view of a binary tree?
The top view of a binary tree is the set of nodes visible from the summit of the tree. Given a binary tree, output its topology. It is possible to publish the output nodes in any order. Node x is included in the output if it is the node with the greatest horizontal distance.
3. Is it possible to determine the left view of a binary tree with a depth-first search (DFS)?
While it's more commonplace to apply a breadth-first search (BFS) or level order traversal to decide the left view, it is feasible to apply a DFS. However, doing so might require retaining a record of the maximum depth you've visited thus far and whether or not a node is the first one at that depth.
Leave a Reply
Your email address will not be published. Required fields are marked *