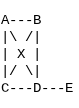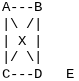Software Key Tutorial
.
Welcome to this tutorial, where we will delve into the subject of bipartite graphs. We'll explore its core aspects, characteristics, and importance in graph theory. A bipartite graph is a fundamental concept in graph theory. Understanding this essential structure opens up a variety of real-world applications, from computer science to operations research.
This tutorial aims to provide an in-depth examination of a bipartite graph in Graph theory. In the subsequent sections, we offer a comprehensive overview of the bipartite graph. We'll discuss definitions, important properties, associated concepts, and end with some commonly asked questions. We'll also delve into their defining features, use cases, and relationship with other types of graphs.
A bipartite graph is a particular type of graph within the broader study of graph theory. Their defining characteristic is that they can be partitioned into two sets such that no two vertices within the same set are adjacent to each other.
Definition and Theory: bipartite graphs, as the name suggests, can be split into two parts. These parts are made in such a way that every edge of the graph connects a vertex in the first part to a vertex in the second part.
Bipartite graph Properties: Some properties of bipartite graphs include that they don't contain odd length cycles and all their cycles have an even number of edges.
Bipartite graph definition with example: Consider the following example: There are two sets of vertices {a, b, c} and {1, 2, 3}. Edges are a-1, b-2, and c-3.
Key Applications: Applications include modeling relationships between different types of objects (like users and groups in social networks), matching problems, and network flows.
A complete graph is a type of graph in which every pair of distinct vertices is connected by a unique edge. In other words, it's a graph where every vertex is directly connected to every other vertex. In the case of a Complete bipartite graph, each node from one set forms a connection with all the nodes of the other set.
Complete graphs are denoted as Kn, where "n" represents the number of vertices.
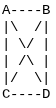
Here is an example of a complete graph with 4 vertices (A, B, C, and D):
In this graph, each vertex is directly connected to every other vertex with a unique edge. For 4 vertices, there are a total of 6 edges. Complete graphs are commonly used in graph theory to illustrate concepts and algorithms due to their simplicity and symmetry.
A regular graph is a graph where all vertices have the same degree, meaning they are connected to the same number of edges. In a regular graph, each vertex has an identical number of adjacent vertices. Regular graphs are often denoted as "k-regular," where "k" is the degree of each vertex.
Here's an example of a 3-regular graph with 4 vertices (A, B, C, and D):
In this graph, each vertex is connected to exactly 3 other vertices, resulting in a regular graph. Regular graphs can have various degrees, and they often represent structured relationships in real-world scenarios.
An Euler Path is a path in a graph that visits every edge exactly once. This means that you start at a vertex, traverse edges to other vertices, and eventually end at a different vertex, covering every edge in the graph without repetition. If you can find an Euler Path in a graph, it suggests a specific sequence in which you can traverse the edges.
However, not all graphs have Euler Paths. There are specific conditions that must be met:
Eulerian Circuit: If the Euler Path starts and ends at the same vertex, it's called an Eulerian Circuit. Not all graphs have Eulerian Circuits either.
Vertex Degrees: In a connected graph, an Euler Path or Eulerian Circuit is possible if and only if there are either 0 or 2 vertices with an odd degree (number of edges incident to the vertex).
For example, let's consider a graph where two vertices have odd degrees (C and E):
In this graph, vertices C and E have an odd degree. This means that an Euler Path or Circuit is not possible. The condition of having either 0 or 2 vertices with odd degrees is violated.
On the other hand, if we modify the graph slightly to ensure there are exactly 2 vertices with odd degrees:
In this case, vertices C and E have an odd degree, which satisfies the condition. An Euler Path (not a circuit) is possible in this graph, where you start at A, traverse all edges, and end at E.
Euler's Theorem states that a graph G has an Euler circuit if and only if every vertex of G has even degree. The theorem holds true for bipartite graphs, as the number of edges incident with a vertex determines whether the vertex's degree is even or odd.
Euler's Theorem Component | Description |
Theorem Statement | A graph G possesses an Euler circuit if and only if every vertex of G has even degree. |
Meaning | A graph has a path that traverses every edge exactly once and returns to its starting point, if and only if each of its vertices is connected to an even number of other vertices. |
Relation with bipartite graphs | The theorem applies to bipartite graphs as the degrees of vertices determine whether an Euler circuit exists. |
Proof Method | The theorem is proved using methods of induction and graph traversal. The proof focuses on the existence of a closed circuit in a graph with vertices of even degree. |
There are several algorithms and techniques to determine if a given graph is bipartite. One common algorithm is the Breadth-First Search (BFS) algorithm.
Here's a step-by-step explanation of how the BFS algorithm can be used to determine if a graph is bipartite:
Choose a Starting Vertex: Start by selecting an arbitrary vertex from the graph as the starting point.
Initialize Vertex Sets: Create two sets, often called "Set A" and "Set B," to store the two disjoint sets of vertices.
Initialize Color Map: Assign colors (often represented as 0 and 1) to the starting vertex. Place the starting vertex in Set A.
Queue Initialization: Enqueue the starting vertex into a queue for BFS traversal.
BFS Traversal:
While the queue is not empty:
Dequeue a vertex from the queue.
Traverse all neighboring vertices of the dequeued vertex.
If a neighboring vertex doesn't have a color assigned:
Assign the opposite color to the neighboring vertex and place it in the respective set.
Enqueue the neighboring vertex into the queue.
If a neighboring vertex has the same color as the current vertex, the graph is not bipartite.
Repeat BFS: Repeat steps 4 and 5 until all vertices have been visited or until a conflict is detected.
Result: If no conflicts arise during BFS traversal (i.e., all edges connect vertices of different colors), the graph is bipartite. If there's a conflict, the graph is not bipartite.
Pseudocode for Bipartite Graph Detection using BFS:
function isBipartite(graph, start_vertex): create sets SetA and SetB create a color map for vertices assign color 0 to start_vertex add start_vertex to SetA create a queue and enqueue start_vertex while queue is not empty: current_vertex = dequeue from queue for each neighbor in graph[current_vertex]: if neighbor is not colored: assign opposite color to neighbor add neighbor to the respective set enqueue neighbor into the queue else if neighbor has the same color as current_vertex: return "Not Bipartite" return "Bipartite" Call isBipartite(graph, any_starting_vertex)
We must also remember that this algorithm assumes the graph is connected. If the graph consists of multiple components, you should apply the BFS algorithm on each component. This algorithm works well for both directed and undirected graphs and is a common approach to determine whether a graph is bipartite or not.
Another method to determine if a graph is bipartite is to use graph coloring with the concept of two-coloring. This method doesn't necessarily require BFS traversal.
Here's how bipartite graph detection works using graph coloring:
Choose a Starting Vertex: Start by selecting an arbitrary vertex from the graph.
Initialize Vertex Colors: Assign colors (often represented as 0 and 1) to the starting vertex. This vertex will be part of Set A.
Color Propagation:
Traverse through the graph's vertices.
For each vertex, if it's not colored:
Assign the opposite color to the vertex.
Traverse all neighboring vertices and assign the opposite color to them as well.
Continue this process until all vertices are colored or until a conflict is detected.
Conflict Detection: If you encounter a vertex that has a neighbor with the same color, the graph is not bipartite.
Result: If no conflicts arise (i.e., all edges connect vertices of different colors), the graph is bipartite.
Pseudocode for Bipartite Graph Detection using Graph Coloring:
function isBipartite(graph, start_vertex): create a color map for vertices assign color 0 to start_vertex for each vertex in graph: if vertex is not colored: assign opposite color to vertex for each neighbor in graph[vertex]: assign opposite color to neighbor if neighbor has the same color as vertex: return "Not Bipartite" return "Bipartite" Call isBipartite(graph, any_starting_vertex)
This method directly assigns colors to vertices based on their adjacency relationships, without explicitly performing BFS traversal. If you don't encounter a conflict during the color propagation process, the graph is bipartite.
We have traversed the fascinating terrain of bipartite graphs, exploring their definition, properties, examples, and related concepts. Understanding bipartite graphs offers a deeper insight into graph theory and its numerous applications. A solid grasp of these concepts not only enhances our problem-solving toolkit but also opens up career opportunities in diverse fields like computer science, data science, and network design. Proficiency in these concepts can set you apart in these competitive industries.
To further elevate your understanding and career, upGrad offers comprehensive courses where such concepts are explained in great detail by industry professionals.
1. Can you provide a bipartite graph example?
Consider a graph with vertices divided into two sets {a, b, c} and {1, 2, 3}. The edges are a-1, b-2, and c-3. This is a bipartite graph.
2. How is a bipartite graph different from a Complete Graph?
In a Complete Graph, each pair of vertices is connected. However, in a Complete bipartite graph, each vertex from one set is connected to every vertex in the other set.
3. What is the relation between a Regular Graph and a bipartite graph?
In a Regular bipartite graph, there are equal vertices in both sets, and each vertex connects to every vertex in the opposite set.
4. How does Euler's Theorem apply to bipartite graphs?
Euler's Theorem states a graph has an Euler circuit if and only if every vertex has an even degree. This also holds true for bipartite graphs.
Leave a Reply
Your email address will not be published. Required fields are marked *