Longest Palindromic Subsequence

Introduction

This article discusses in detail the concept of the Longest Palindromic Subsequence. This is a powerful tool in the world of programming, especially when working with Java and C++. It might sound complex, but to make it simple, we're going to break it down into easy-to-understand steps.

A palindrome is a sequence that reads the same way backward and forward, like "MADAM". A palindromic subsequence is a subsequence from a string, which is a palindrome. The longest palindromic subsequence is the one with the maximum length.

This algorithmic concept is useful in a lot of computing fields, including data analysis, game development, and Machine Learning. It improves the efficiency and speed of various computing operations.

Overview

In this tutorial, we'll focus on the Longest Palindromic Subsequence. It's a concept that's applicable in various programming languages, including Java, C++, and Python.

We'll teach you how to print the Longest Palindromic Subsequence. This is a fundamental step in understanding the process. We'll make it simple for you to see the output and understand how the algorithm works.

Moving on, we'll delve into the longest palindromic subsequence in Python. Python is an excellent language for learning this concept because of its easy-to-understand syntax. We'll guide you through the steps to implement this concept in Python and help you understand the underlying logic.

C++ is a robust language that offers many features for efficient coding. We'll show you how to code the Longest Palindromic Subsequence in C++ in an easy-to-follow way.

We'll wrap up with a discussion on Striver's approach to the Longest Palindromic Subsequence. Striver's method is popular, breaking down the problem into more manageable parts. It's an excellent approach for those who want to deepen their understanding of this topic.

Problem Statement

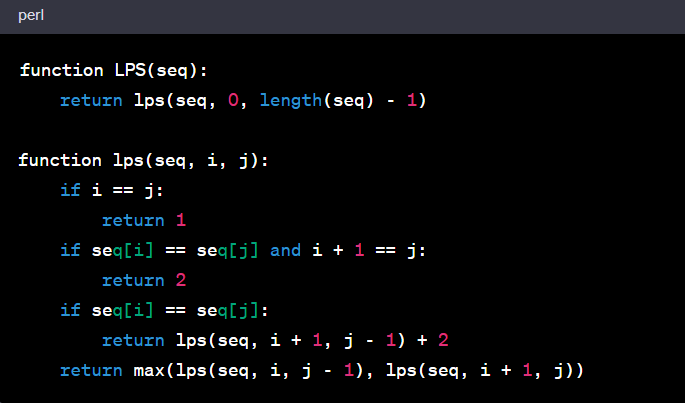
Problem Statement 1:

Given a string, we want to find the length of the Longest Palindromic Subsequence (LPS). A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

For example, in the string "BBABCBCAB", the longest palindromic subsequence is "BABCBAB", so the output should be 7.

Constraints:

• The string will contain only uppercase or lowercase English letters.
• The length of the string will be at most 1000.

Use the Recursive Approach.

Algorithm:

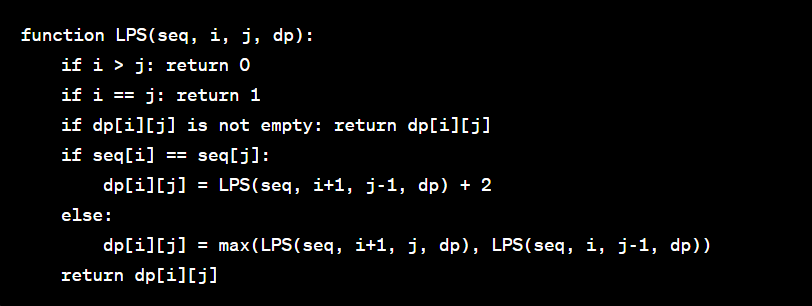
1. Create a helper function, lps, which calculates the length of the longest palindromic subsequence in the substring seq[i...j].
2. If seq[i] equals seq[j], the length of the LPS is the same as the one in seq[i+1...j-1] plus 2.
3. Otherwise, the length of the LPS is the maximum of that of the one in seq[i+1...j] and seq[i...j-1].
4. The length of the LPS in the entire string seq is lps(seq, 0, length(seq) - 1).

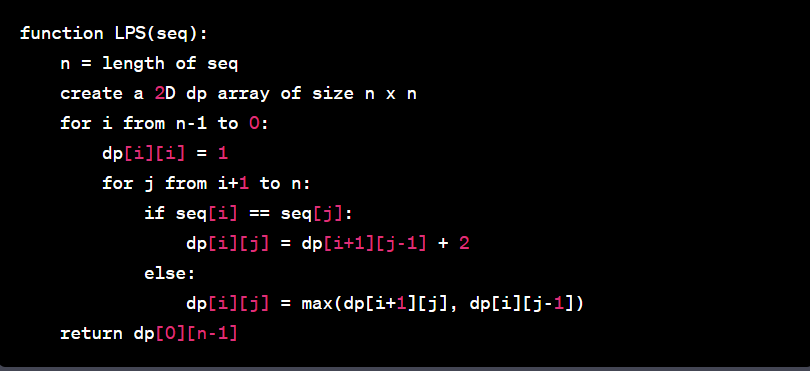
Pseudocode:

Output: "The length of the LPS is 5."

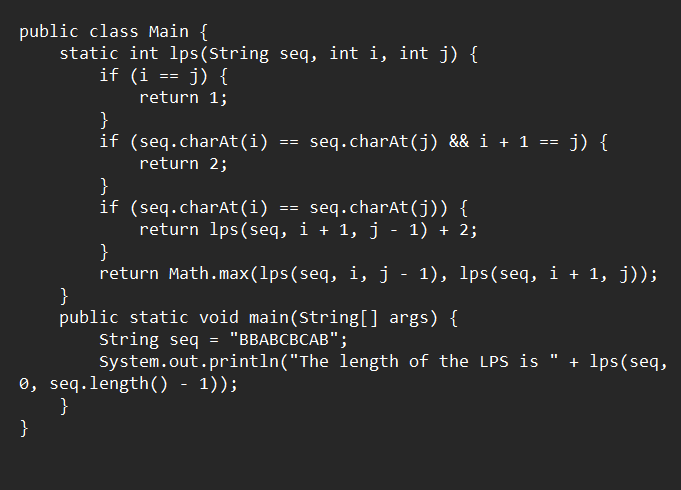
Java Implementation (Recursive Approach)

Java Output: "The length of the LPS is 7."

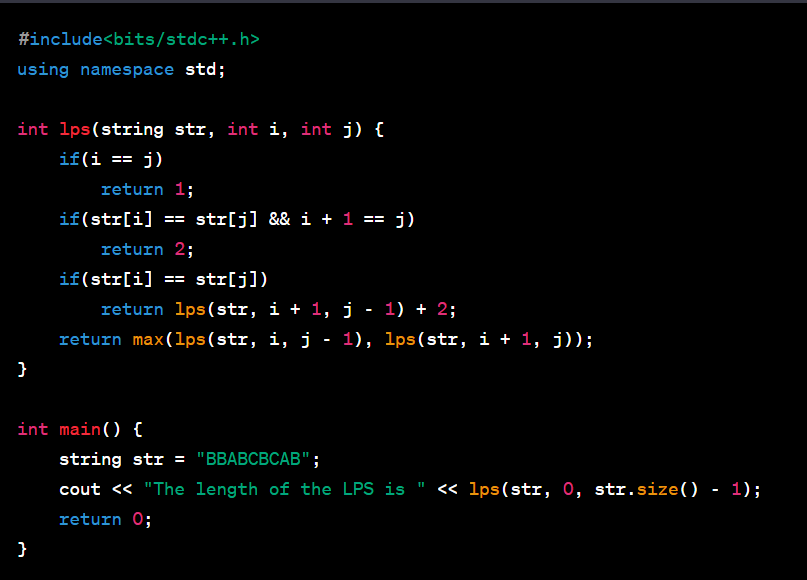
C++ Implementation (Recursive Approach)

C++ Output: "The length of the LPS is 7"

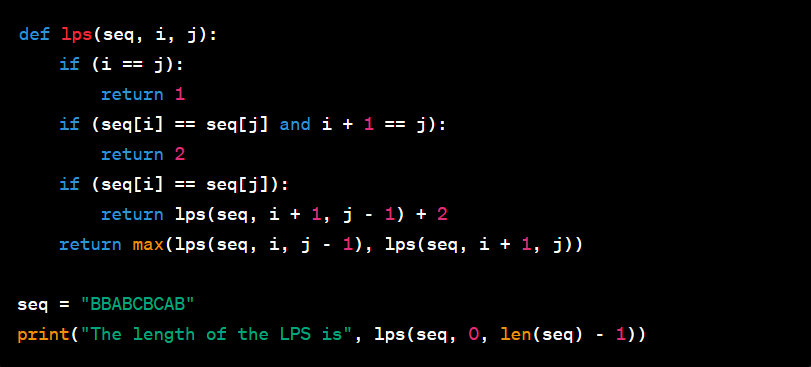
Python Implementation (Recursive Approach)

Python Output: "The length of the LPS is 7"

Problem Statement 2

Given a string, we have to find the length of the Longest Palindromic Subsequence (LPS).

For example, in the string "GEEKSFORGEEKS", the longest palindromic subsequence is "EEGEE", so the output should be 5.

Constraints:

• The string will contain only uppercase English letters.
• The length of the string will be at most 100.

Use the Bottom-up Dynamic Programming (DP) approach for this problem.

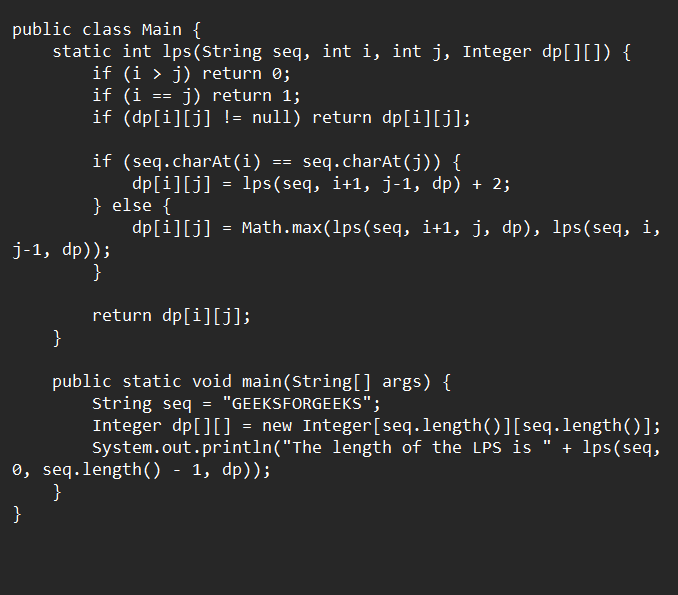
Algorithm:

1. Build a 2D dp table, where each cell dp[i][j] represents the length of the longest palindromic subsequence in the substring seq[i...j].
2. If seq[i] equals seq[j], dp[i][j] is the length of the LPS in seq[i+1...j-1] plus 2.
3. Otherwise, dp[i][j] is the maximum of dp[i+1][j] and dp[i][j-1].
4. The length of the LPS in the entire string seq is dp[0][length(seq) - 1].

Pseudocode:

Dry Run ( Bottom-Up Dp)

A dry run is a step-by-step, manual execution of a code to understand its flow and verify its correctness. Here's how you would do a dry run for the Bottom-up Dynamic Programming approach using the string "GEEKS" as an example:

1. Start with a string "GEEKS" of length 5.
2. Create a 2D array dp of size 5x5 to store the length of the longest palindromic subsequence in the substring seq[i...j].

Here's how dp would initially look (0's indicate that these cells have not been calculated yet):

1. Starting from the string's last character, fill the dp table diagonally. Every dp[i][i] is 1 because a single character is a palindrome of length 1.

Here's how dp would look like after this step:

2. Now, fill the rest of the dp table row by row. When filling dp[i][j], if seq[i] equals seq[j], set dp[i][j] to dp[i+1][j-1] + 2. Otherwise, set it to the maximum of dp[i+1][j] and dp[i][j-1].

Here's how dp would look like after this step:

3. The length of the longest palindromic subsequence in the entire string seq is dp[0][4], is 2. So, the final output is 2.

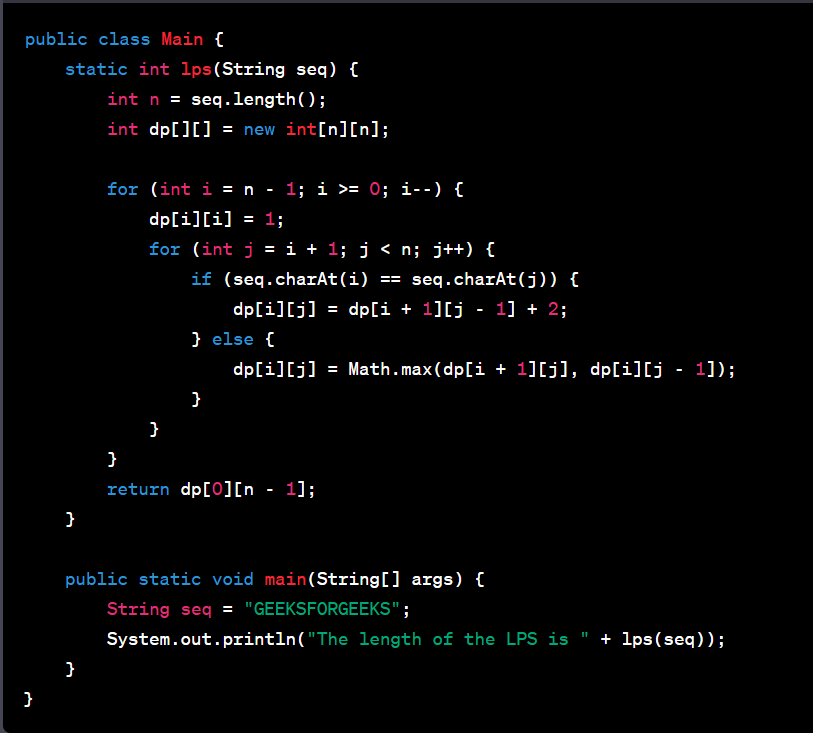
Java Implementation (Bottom-up DP)

Java Output: "The length of the LPS is 5"

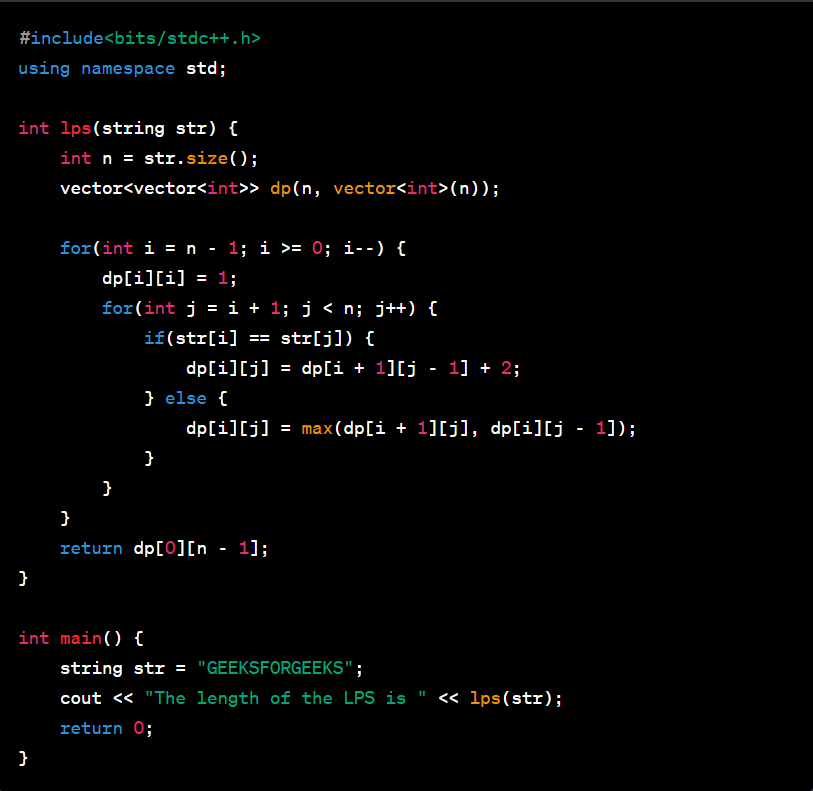
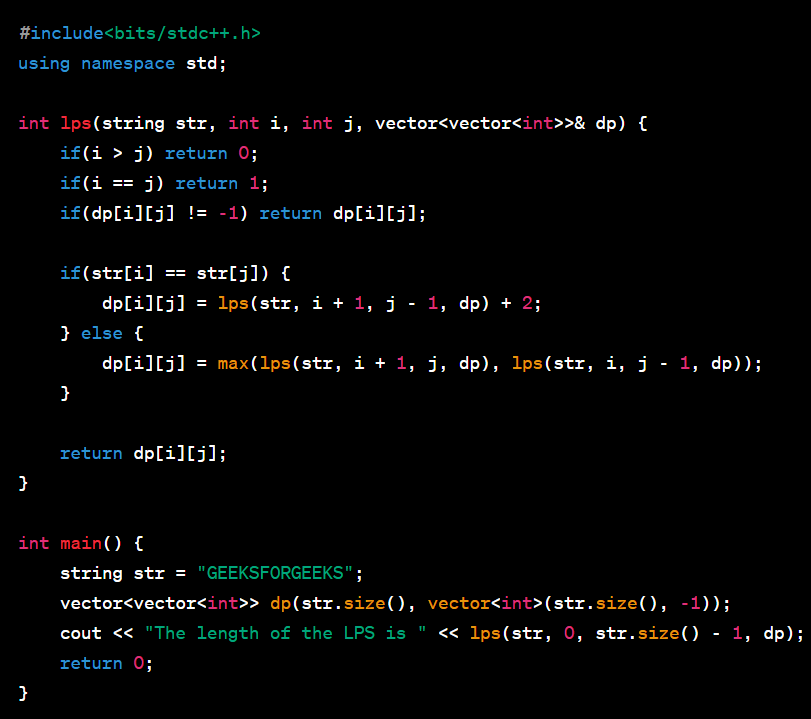
C++ Implementation (Bottom-up DP)

C++ Output: "The length of the LPS is 5"

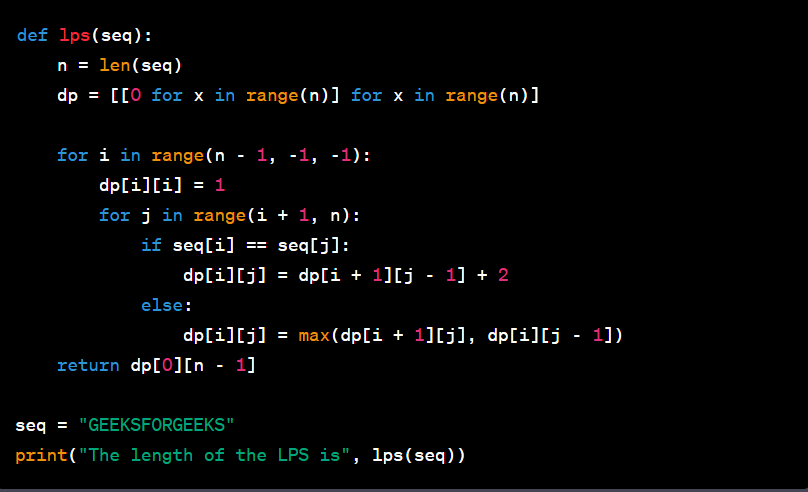
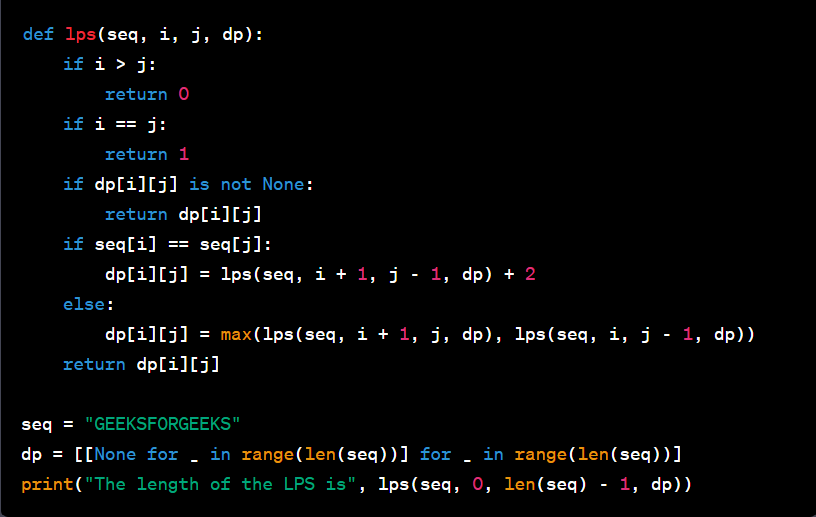
Python Implementation (Bottom-up DP)

Python Output: "The length of the LPS is 5"

Complexity Analysis

The complexity analysis of the bottom-up dynamic programming approach for the longest palindromic subsequence problem is as follows:

Time Complexity: The time complexity is O(n^2), where ‘n’ is the length of the input string. This is because our approach is filling a 2D table of size n x n. Each cell of the table is filled in constant time, and there are n^2 cells in total, so the time complexity is O(n^2).

Space Complexity: The space complexity is also O(n^2) because we are using a 2D table of size n x n to store the intermediate results. Each cell of this table stores an integer, and there are n^2 such cells. Thus, the space required is proportional to n^2, leading to a space complexity of O(n^2).

Memoization Approach

Memoization is a powerful technique used in computer programming to optimize the execution speed of a program by storing the results of expensive function calls and reusing them when the same inputs occur again.

Here are some key functions of memoization:

1. Caching Results
2. Avoiding Redundant Computations
3. Improving Time Complexity
4. Space Tradeoff
5. Top-down Approach

In this method, we start with the naive recursive solution but add a way to store the results of overlapping subproblems to avoid recomputation.

Pseudocode:

Java Implementation (Memoization)

Java Output: "The length of the LPS is 5"

C++ Implementation (Memoization)

C++ Output: "The length of the LPS is 5"

Python Implementation (Memoization)

Output: "The length of the LPS is 5"

Complexity Analysis

1. Time Complexity: The time complexity of this approach is O(n^2), where n is the length of the input string. This is because we are utilizing memoization to store the results of overlapping subproblems, so each one is computed only once. There are a total of n^2 possible subproblems, so the total time complexity is O(n^2).

2. Space Complexity: The space complexity is also O(n^2). We use a 2D dp array to store the solutions of all the subproblems, and there are a total of n^2 subproblems. Thus, the total space needed is proportional to n^2, resulting in a space complexity of O(n^2).

Longest Palindromic Subsequence

The Longest Palindromic Subsequence (LPS) problem involves finding the longest subsequence of a given sequence such that the subsequence is a palindrome. For instance, consider the sequence "GEEKSFORGEEKS". The longest palindromic subsequence would be "EEKEE", which has a length of 5.

Optimal Substructure

The LPS problem exhibits the optimal substructure property, which means the optimal solution to the problem can be constructed from the optimal solutions of its subproblems.

Example:

Let's say we have the sequence "ABBDCACB". The LPS is "BCACB", which has a length of 5.

If we consider a subproblem by removing the first and last characters from the sequence, we get "BBDCAC". The LPS of this subsequence is also "BCACB", which is of length 5.

So, the optimal solution of the subsequence is part of the optimal solution of the main sequence. This property is referred to as the optimal substructure property.

Overlapping Subproblems

The LPS problem also has overlapping subproblems, which means the same subproblems are solved multiple times. This happens because, while finding the LPS of the given sequence, we end up solving the same smaller problems repeatedly.

For example, while calculating the LPS for the sequence "ABBDCACB", we need to calculate the LPS for the subsequence "BBDCAC" twice, once after removing the first character and then after deleting the last character.

This overlapping of subproblems is a cue that we can improve our algorithm by using techniques like dynamic programming or memoization to store the results of subproblems and avoid solving them multiple times. This leads to a much more efficient algorithm than the naive recursive solution.

Conclusion

The Longest Palindromic Subsequence Problem is a classic example of a problem solvable with dynamic programming. It shows the power of this method in dealing with optimization problems, especially when the problem exhibits properties like overlapping subproblems and optimal substructure.

The bottom-up and the top-down approach with memoization provide an efficient solution, reducing the time complexity to O(n^2) from the exponential time complexity of the naive recursive solution. However, they also increase the space complexity to O(n^2) due to the use of a 2D dp table or memoization.

FAQs

1. What's the significance of printing the longest palindromic subsequence in programming challenges?

Printing the longest palindromic subsequence, rather than just its length, is often asked in programming challenges and interviews. It allows evaluators to see your understanding of dynamic programming concepts and your ability to manipulate and use data structures to retrieve and display information.

2. How does the longest palindromic subsequence problem relate to other dynamic programming problems?

The longest palindromic subsequence problem shares features with other well-known dynamic programming problems like the Longest Common Subsequence (LCS) and the Longest Increasing Subsequence (LIS). They all demonstrate optimal substructure and overlapping subproblems, two key properties that make dynamic programming an ideal solution.

3. Why do we use a 2D array for memoization in the longest palindromic subsequence problem?

We use a 2D array for memoization in this problem because we need to store the results of subproblems that involve two indices . Each cell in the array stores the length of the longest palindromic subsequence for a particular subsequence of the input.

4. What are some common mistakes or challenges when solving the longest palindromic subsequence problem?

One common mistake is not handling the base cases properly, particularly the situation where a single character is a valid palindrome. Correctly setting up the memoization or dynamic programming table is a challenge.