Armstrong Number

Introduction

Today, we'll be exploring a unique category of numbers known as Armstrong numbers. But what exactly is it? It's a number that equals the sum of its own digits, each raised to the power of the number of digits.

Now, you might be wondering how to find Armstrong numbers. That's where the "Armstrong number program" comes in handy. With programming languages like Java and C++, you can create a program to identify these intriguing numbers. Whether you're a Math enthusiast or a programming beginner, this concept offers an exciting opportunity to blend number theory with coding.

Overview

In this guide, we'll touch upon different aspects of Armstrong numbers. We'll start with the "Armstrong number in Java", looking at how this powerful language helps identify these unique numbers. Next, we'll dive into Python to see how "Armstrong Number Python" programs work.

Of course, we can't leave out C and C++, two foundational languages in the programming world. We'll explore the specifics of creating an "Armstrong number in C" program and see how "Armstrong number C++" programs work. We'll also discuss how to perform an "Armstrong number check" to verify these digits.

What is an Armstrong Number in C?

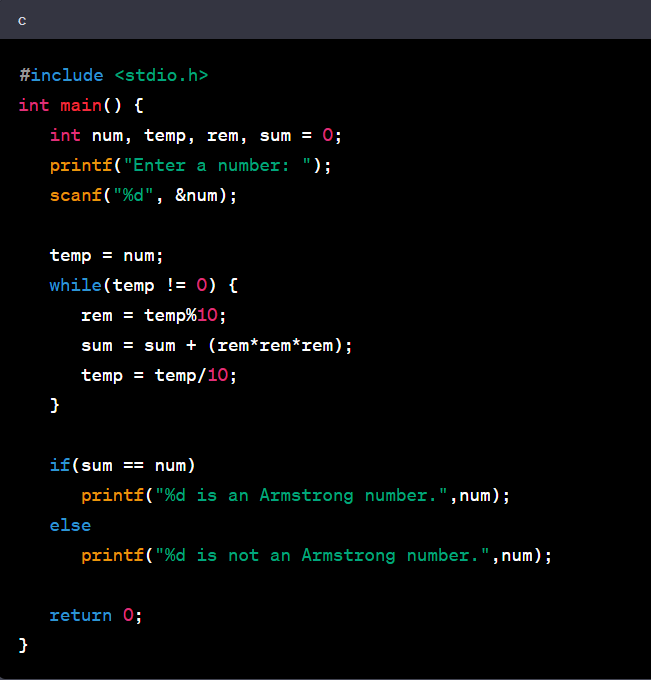
In the C programming language, an Armstrong number is a number that is equal to the sum of the cubes of its digits. For example, 153 is an Armstrong number because 1^3+ 5^3 + 3^3 = 153.

Here's a simple C program to check if a number is an Armstrong number:

Here, you enter a number. The program then splits it into its individual digits, cubes them, and adds them together. If the resulting sum equals the original number, the program will tell you that it's an Armstrong number. If not, it will say it's not an Armstrong number.

Output:

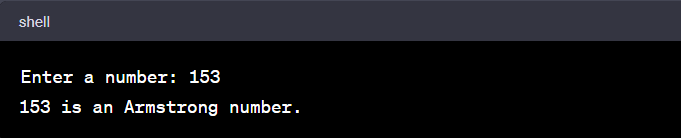
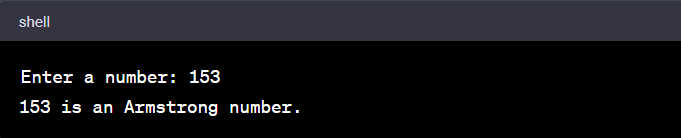
When you run the above C program, it will ask for a number. Let's say you enter '153'. Here's what you would see in your command-line interface:

In this case, the program recognizes '153' as an Armstrong number because the sum of the cubes of its digits equals the original number (1^3 + 5^3 + 3^3 = 153).

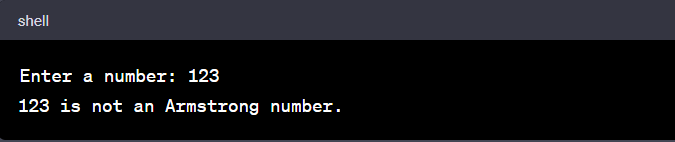
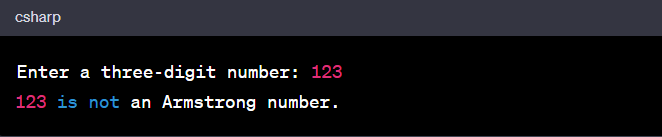
If you enter a non-Armstrong number, let's say '123', the output would be:

Here, the sum of the cubes of its digits does not equal the original number (1^3 + 2^3 + 3^3 = 36), so '123' is not an Armstrong number.

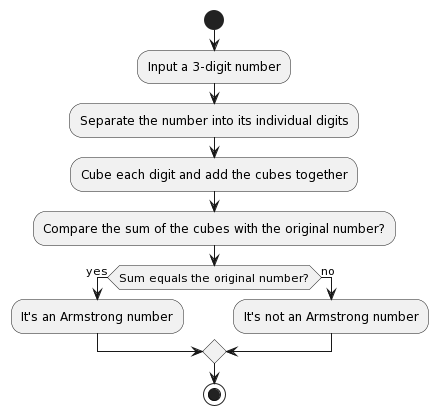
Algorithm for Armstrong Number (3-Digit)

Here is a simple algorithm for finding a 3-digit Armstrong number.

Flowchart for the Armstrong Number (3-Digit):

Example:

Take 371.

1. Separate it into digits: 3, 7, 1.
2. Cube each digit and add: 3^3 + 7^3 + 1^3 = 27 + 343 + 1 = 371.
3. Since the result equals the original number (371), it's an Armstrong number.

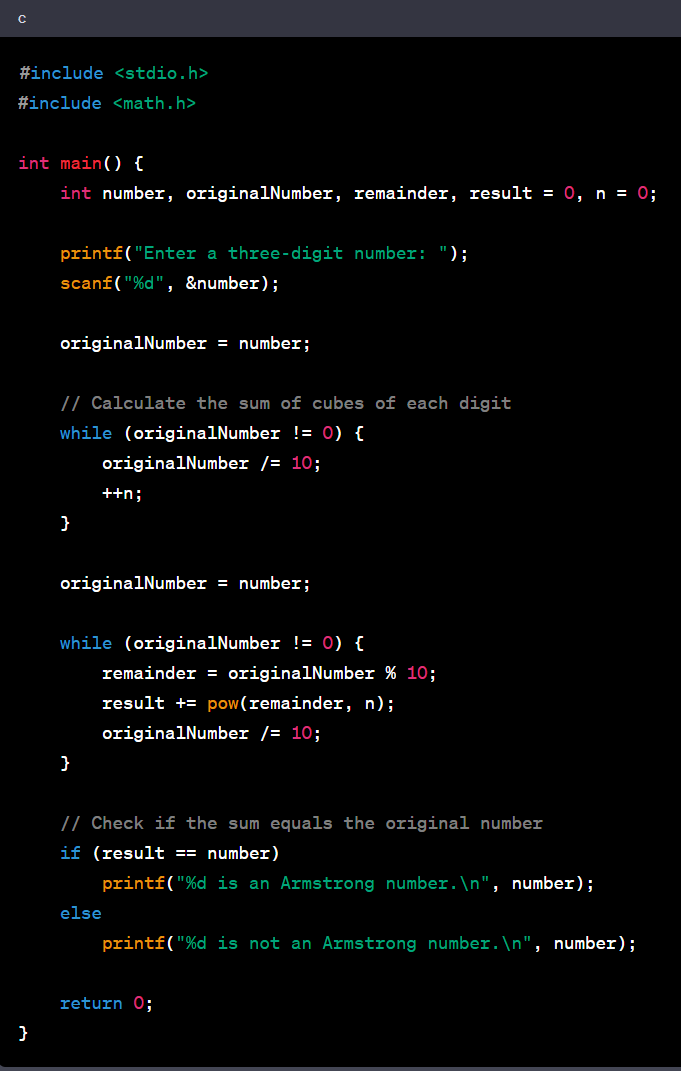
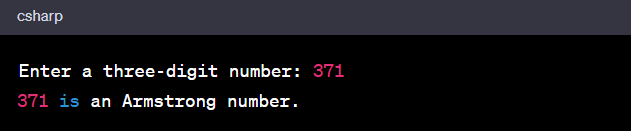
Armstrong Number Program in C for Three-Digit Number

An example of a C program that checks whether a three-digit number is an Armstrong number or not.

Output:

And for the input number 123:

Armstrong Number in Java for Three-Digit Number

The Armstrong Number in Java for a three-digit number allows one to determine whether a given number is an Armstrong number. Possible uses of this program are:

1. Educational purposes
2. Number validation
3. Algorithm validation
4. Code snippet integration
5. Automated testing

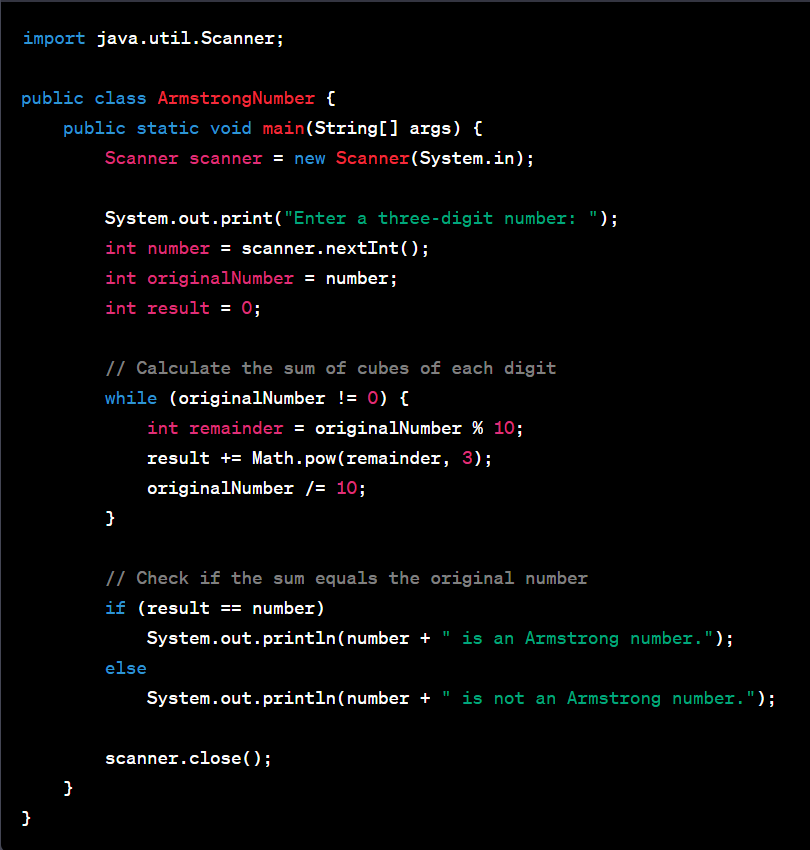
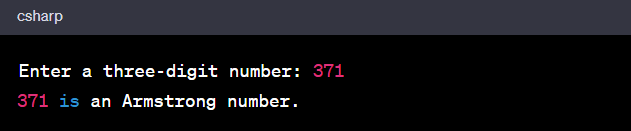
Here's an example of a Java program that checks whether a three-digit number is an Armstrong number or not.

Output:

Here, the program calculated the sum of the cubes of each digit: 3^3 + 7^3 + 1^3 = 27 + 343 + 1 = 371. Since it is equal to the original number, the program determined that it is an Armstrong number and displayed the corresponding message.

Explanation:

1. The program starts by importing the necessary classes, including the Scanner class, for user input.
2. The main method is defined as the entry point of the program.
3. A Scanner object is created to read user input from the console.
4. The user is prompted to enter a three-digit number using the System.out.print statement.
5. The user's input is stored in the variable number using the scanner.nextInt() method.
6. The original input is stored in the variable originalNumber to be used later.
7. The variable result is initialized to 0 and will be used to store the sum of cubes of each digit.
8. The program enters a loop that calculates the sum of cubes of each digit. In each iteration, the remainder of originalNumber is divided by 10 and stored in the remainder. The cube of the remainder is added to the result. Finally, originalNumber is divided by 10 to move to the next digit.
9. After the loop finishes, the program checks whether the result is equal to the original number. If they are, it means the number is an Armstrong number. Otherwise, it's not.
10. The program outputs the appropriate message to the console using System.out.println.
11. The Scanner is closed to free system resources.

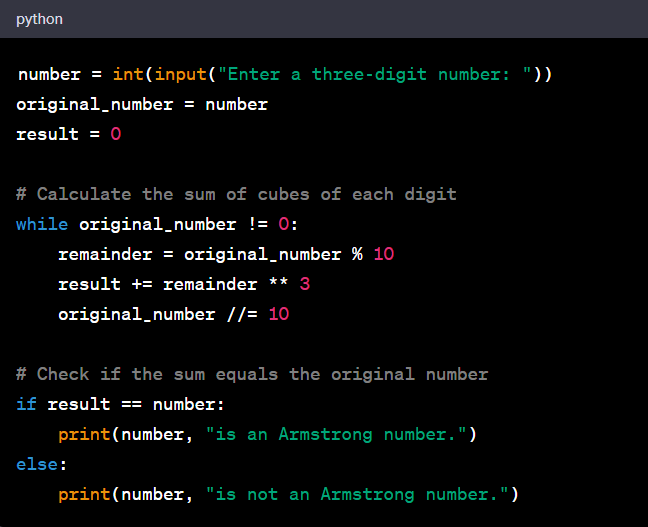
Armstrong Number Program in Python For Three-Digit Number

Here's an example of a Python program that checks whether a three-digit number is an Armstrong number or not.

output for input number 371:

Here, the program calculated the sum of the cubes of each digit: 3^3 + 7^3 + 1^3 = 27 + 343 + 1 = 371. Since it is equal to the original number, the program determined that it is an Armstrong number and displayed the corresponding message.

Explanation:

1. The program prompts the user to enter a three-digit number using the input function.
2. The user's input is converted to an integer using int() and stored in the variable number.
3. The variable original_number is assigned the value of the number to preserve the original input.
4. The variable result is initialized to 0 and will be used to store the sum of cubes of each digit.
5. The program enters a loop that calculates the sum of cubes of each digit. In each iteration, the remainder of the original_number is divided by 10 and stored in the remainder. The cube of the remainder is added to the result. Finally, the original_number is divided by 10 using the floor division operator // to move to the next digit.
6. After the loop finishes, the program checks whether the result is equal to the original number. If they are, it means the number is an Armstrong number. Otherwise, it's not.
7. The program outputs the appropriate message to the console using the print function.

Armstrong Number C++

Here's a program in C++ to check if a number is an Armstrong number:

When you run the C++ program, it will ask for a number. Let's say you enter '9474'. Here's what you would see on your console:

In this case, the program recognizes '9474' as an Armstrong number because the sum of the 4th power of its digits equals the original number (9^4 + 4^4 + 7^4 + 4^4 = 9474).

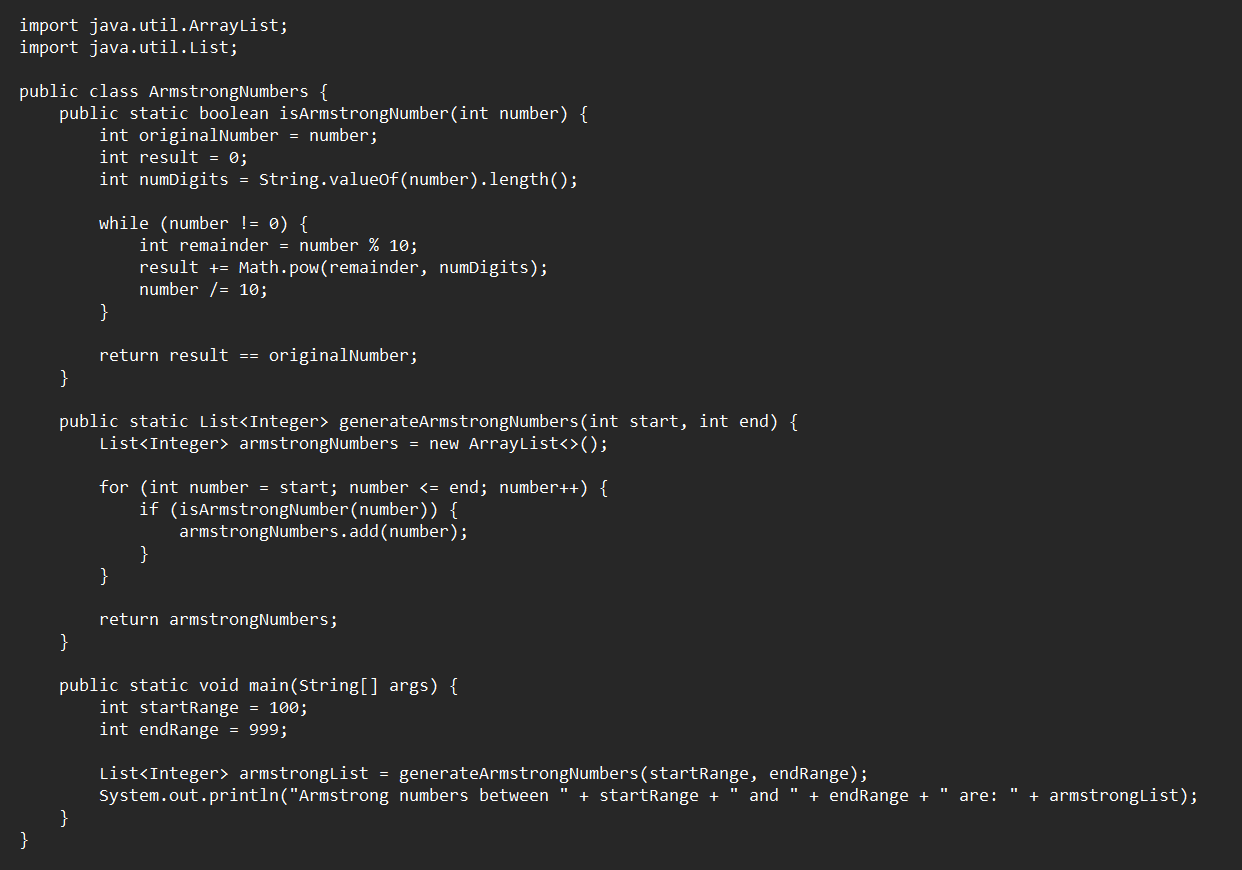
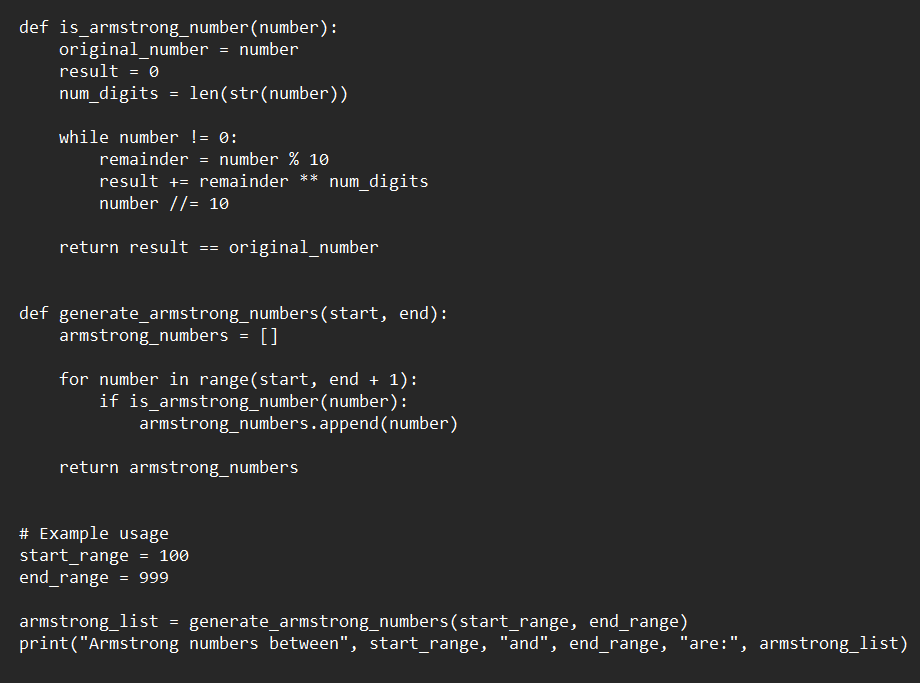
Armstrong Number List Program Implementation In Java, Python, And C++

Java

Output:

Python

Output:

C++

Output:

Analysis of Algorithms With C++, Java, And Python

1. C++:

The C++ algorithm receives a number as input and calculates its length. Then, it splits the number into individual digits, raises each digit to the power of the number's digit count, and adds them together. If the resulting sum equals the original number, the program prints that it's an Armstrong number. Otherwise, it's not.

This algorithm has a time complexity of O(n), where n is the number of digits. This is because each digit is processed individually.

For example, with the number 9474, the algorithm calculates the length (4), then processes each digit: 9^4, 4^4, 7^4, 4^4. Since the sum equals the original number, it outputs that 9474 is an Armstrong number.

2. Java:

The Java algorithm is very similar to the C++ one. The difference lies in the specific syntax and conventions of Java, such as the use of the Math.pow function for exponentiation and Scanner for input.

Its time complexity is also O(n), for the same reasons as the C++ algorithm.

3. Python:

The Python algorithm is more concise due to Python's built-in functions and simple syntax. It uses the len() function to find the number of digits and ** for exponentiation.

The time complexity is also O(n), just like the other two algorithms.

In all three languages, the algorithms break the number down into individual digits and perform calculations on each. The only difference is due to each language's specific syntax and features.

Time Complexity

It is a concept in Computer Science that deals with the amount of computational time taken by an algorithm to run as a function of the size of the input to the program. It's generally expressed using Big O notation, which describes the upper bound of the time complexity in the worst-case scenario.

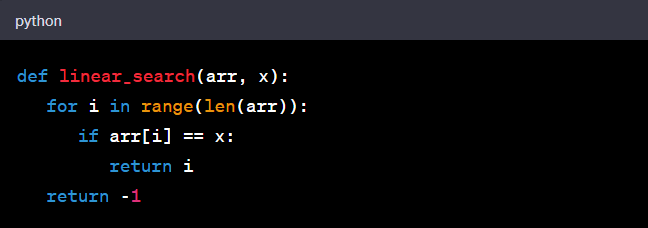
Let's consider a simple linear search algorithm in Python.

The time complexity of this algorithm is O(n), where 'n' is the length of the array. This is because, in the worst-case scenario (when the element is not in the array), the algorithm would need to traverse the entire array.

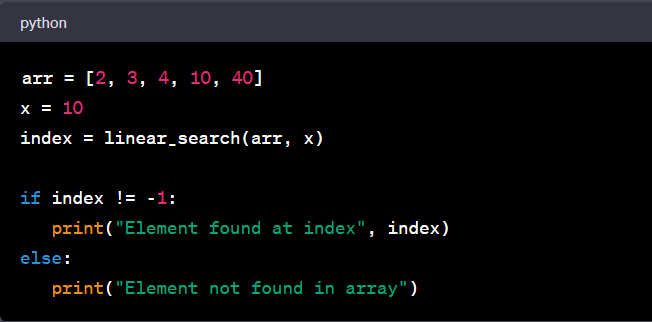
If you run the linear search function with an array and a search element, you get the index of the element if it is in the array or -1 if it is not.

For example:

Output:

Space Complexity

It is another concept in Computer Science that represents the amount of memory an algorithm needs to run to completion. It's often expressed using Big O notation.

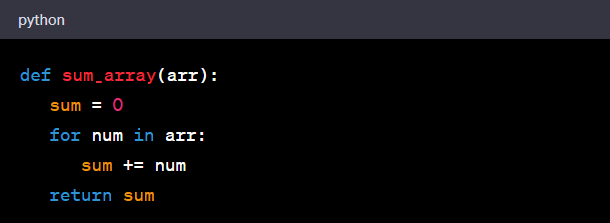
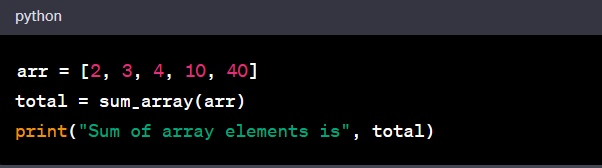
Let's consider a simple algorithm that sums the elements in an array:

In this case, the space complexity is O(1), which means the memory required by the algorithm is constant, regardless of the size of the array. This is because the algorithm only uses one variable (sum) to hold the total, and this doesn't change regardless of the size of the input array.

When you run the sum array function with an array as input, you get the sum of the elements in the array. For example,

Output:

Conclusion

Understanding the concept of Armstrong numbers and how to implement their identification in various programming languages like C++, Java, and Python is an important skill for every programmer. These provide hands-on knowledge about loops, conditionals, and mathematical operations, all of which are fundamental to programming.

FAQs

1. What are some real-world applications of Armstrong numbers?

These numbers are largely theoretical and used for educational purposes to understand programming and number theory concepts. Even so, they come up in checksum algorithms where having a number's individual digits contain information about the whole is beneficial.

2. Why are Armstrong numbers also known as Narcissistic numbers?

The term "Narcissistic number" comes from the Greek myth of Narcissus, who fell in love with his own reflection. Similarly, Armstrong numbers can be "in love with themselves," as they can be expressed as a combination of their own digits raised to the power of the number of digits.

3. What would be an efficient method to generate all Armstrong numbers with n digits?

An efficient method to generate all Armstrong numbers of n digits would be to use a nested loop where the outer loop goes from 1 to n. The inner loop generates all n-digit numbers and checks if they are Armstrong numbers.

4. What is an example of a 4-digit Armstrong number, and how can we identify such numbers?

A classic example is 9474 because 9^4 + 4^4 + 7^4 + 4^4 equals 9474. To identify a 4-digit Armstrong number, we could write a program that takes a four-digit number as input, raises each digit to the fourth power, adds those values together, and then checks if the resulting sum equals the original number.