Software Key Tutorial
.
In the realm of data communication and storage, ensuring data integrity is of paramount importance. One of the most widely used error-detection techniques is the Cyclic Redundancy Check (CRC) algorithm. This powerful method plays a vital role in detecting errors during data transmission, storage, and retrieval.
In this comprehensive guide, we'll explore the intricacies of CRC, its working principles, and real-life examples to understand how it safeguards data integrity.
The Cyclic Redundancy Check (CRC) is an error-detection technique used in various fields, including computer networks, data storage systems, and communication protocols. It involves appending a fixed number of bits (the CRC checksum) to the data being transmitted or stored.
Upon reception or retrieval, the recipient can calculate its own CRC checksum and compare it with the received one to determine if any errors occurred during transmission.
A Cyclic Redundancy Check (CRC) is an error-detection algorithm widely used in computer networks, data storage systems, and communication protocols. Its primary purpose is to detect errors during data transmission, storage, or retrieval processes.
The CRC algorithm involves performing polynomial division on the data and generating a fixed-size checksum, which is appended to the data before transmission or storage. Upon receiving the data, the recipient can independently calculate its CRC checksum and compare it with the received ones. If both checksums match, the data is considered to be error-free. However, if the checksums differ, it indicates that errors have occurred during data transmission, and the data integrity may be compromised.
CRC operates by utilizing a predetermined binary polynomial, known as the CRC polynomial or generator polynomial. The choice of the polynomial impacts the algorithm's effectiveness in detecting errors of different types and magnitudes.
This error-detection technique provides a reliable means to verify the accuracy of transmitted or stored data. It is essential in various applications, including internet communication, wireless networks, file transfers, and disk storage systems. The use of CRC ensures data integrity, critical for maintaining the overall reliability and efficiency of digital information exchange.
Let's understand this with an example:
Cyclic redundancy check example 1: Cyclic redundancy check calculator
Suppose we want to send the 8-bit data: 01100101. Using a predetermined CRC polynomial, let's say x^3 + x^2 + 1 (expressed as 1011 in binary), we perform CRC calculation:
Step 1: Append 3 zeros (the number of bits in the CRC polynomial minus 1) to the data:
01100101000
Step 2: Perform modulo-2 division on the augmented data with the CRC polynomial:
1001 (Divisor: CRC Polynomial)
-----------------
01100101000
1001
-----------------
11100
1001
-----------------
10110
1001
-----------------
10111 (Remainder: CRC Checksum)
Step 3: Append the remainder (CRC checksum) to the original data:
0110010110111
Now, the data to be transmitted is 0110010110111, where the last 4 bits represent the CRC checksum.
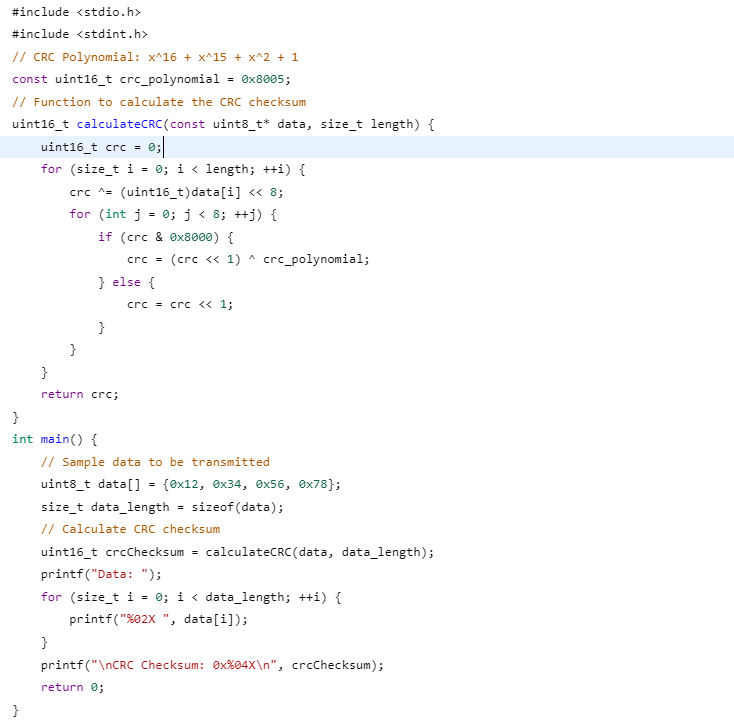
Below is a simple implementation of the Cyclic Redundancy Check (CRC) algorithm in C++ for error detection. This example uses a common CRC polynomial, which is x^16 + x^15 + x^2 + 1 (expressed as 0x8005 in hexadecimal or 10000000000000011 in binary).
Output:
In this code, the calculateCRC function takes an array of bytes (data) and its length as input and returns the calculated CRC checksum as a 16-bit unsigned integer. The main function demonstrates how to use the calculateCRC function to calculate the CRC checksum for a sample data array (data) and then prints both the data and the resulting CRC checksum in hexadecimal format.
Before we delve deeper, let's familiarize ourselves with some essential CRC terms and attributes:
CRC Polynomial: It is a predetermined binary pattern used in the CRC calculation. Different polynomials result in varying levels of error-detection capability.
Generator Polynomial: The CRC polynomial, often represented in binary form.
Degree of the Polynomial: The highest power in the CRC polynomial, determining the number of bits in the CRC checksum.
Checksum: The remainder obtained after performing the CRC division, used for error detection.
Check Value: The CRC checksum appended to the data before transmission.
Syndrome Table: A lookup table used for faster CRC calculations.
The CRC algorithm operates at both the sender and receiver sides during data transmission. Let's explore each step in detail:
Sender Side (CRC Generator and Modulo Division)
At the sender side, the CRC algorithm generates the CRC checksum and appends it to the data before transmitting it to the receiver. The steps involved are as follows:
Step 1: Augmentation - Append zeros to the data equal to the degree of the CRC polynomial minus one.
Step 2: Modulo Division - Perform polynomial division (modulo-2 division) on the augmented data with the CRC polynomial.
Step 3: Append the remainder (CRC checksum) to the original data.
Let's take another real-life example to understand this better.
Cyclic redundancy check example 2: CRC Generation
Suppose we have a 16-bit data packet: 1010101011001100. The CRC polynomial used is x^4 + x^3 + 1 (expressed as 11001 in binary).
Step 1: Augment the data with 3 zeros (degree of the polynomial is 4, so we append 4 - 1 = 3 zeros):
1010101011001100000
Step 2: Perform modulo-2 division with the CRC polynomial:
11001
-----------------
1010101011001100000
11001
-----------------
1010101011000001101 (Remainder: CRC Checksum)
Step 3: Append the CRC checksum to the original data:
1010101011001100101
Now, the data to be transmitted is 1010101011001100101, where the last 4 bits represent the CRC checksum.
Receiver Side (Checking for Errors in the Received Data)
On the receiver side, the CRC algorithm verifies the integrity of the received data. The process involves calculating the CRC checksum using the same polynomial and comparing it with the received checksum. If they match, the data is considered error-free; otherwise, errors are detected.
Step 1: Augmentation - Append zeros to the received data equal to the degree of the CRC polynomial minus one.
Step 2: Modulo Division - Perform polynomial division (modulo-2 division) on the augmented received data with the CRC polynomial.
Step 3: The data is error-free if the remainder obtained matches the received CRC checksum. Otherwise, errors are detected.
Let's continue with our previous example to see how error detection works.
3. Cyclic redundancy check error detection
Suppose during transmission, the data packet 1010101011001100101 is received with errors, resulting in 1010101011000100101.
Step 1: Augment the received data with 3 zeros:
1010101011000100101000
Step 2: Perform modulo-2 division with the CRC polynomial:
11001
-----------------
1010101011000100101000
11001
-----------------
1010101011000001101010 (Remainder: Calculated CRC Checksum)
Step 3: Compare the calculated CRC checksum (1010) with the received CRC checksum (0101). As they don't match, errors are detected.
Cyclic redundancy check in computer networks is commonly used in the Data Link Layer to ensure reliable data transmission. It is employed in protocols like Ethernet, PPP, HDLC, and others. In this context, CRC plays a pivotal role in detecting accidental bit flips or errors introduced during data transmission over the network.
Here's a complete C++ implementation of the Cyclic Redundancy Check (CRC) algorithm for error detection. This implementation uses a common CRC polynomial, which is x^16 + x^15 + x^2 + 1 (expressed as 0x8005 in hexadecimal or 10000000000000011 in binary).
#include <iostream>
#include <cstdint>
#include <cstring>
// CRC Polynomial: x^16 + x^15 + x^2 + 1
const uint16_t crc_polynomial = 0x8005;
// Function to calculate the CRC checksum
uint16_t calculateCRC(const uint8_t* data, size_t length) {
uint16_t crc = 0;
for (size_t i = 0; i < length; ++i) {
crc ^= (uint16_t)data[i] << 8;
for (int j = 0; j < 8; ++j) {
if (crc & 0x8000) {
crc = (crc << 1) ^ crc_polynomial;
} else {
crc = crc << 1;
}
}
}
return crc;
}
int main() {
// Sample data to be transmitted
uint8_t data[] = {0x12, 0x34, 0x56, 0x78};
// Calculate CRC checksum
uint16_t crcChecksum = calculateCRC(data, sizeof(data));
std::cout << "Data: ";
for (size_t i = 0; i < sizeof(data); ++i) {
std::cout << std::hex << (int)data[i] << " ";
}
std::cout << "\nCRC Checksum: 0x" << std::hex << crcChecksum << std::endl;
// Simulate data transmission with errors
data[2] = 0xAB;
uint16_t receivedChecksum = calculateCRC(data, sizeof(data));
std::cout << "Received Data with Error: ";
for (size_t i = 0; i < sizeof(data); ++i) {
std::cout << std::hex << (int)data[i] << " ";
}
std::cout << "\nReceived CRC Checksum: 0x" << std::hex << receivedChecksum << std::endl;
// Verify if errors occurred during transmission
if (receivedChecksum == crcChecksum) {
std::cout << "No errors detected during transmission.\n";
} else {
std::cout << "Errors detected during transmission!\n";
}
return 0;
}In this code, the calculateCRC function calculates the CRC checksum for a given data array. The main function demonstrates how to use this function to calculate the CRC checksum for a sample data array and then simulate data transmission with errors by modifying one of the data bytes.
It then recalculates the CRC checksum for the modified data and verifies if errors were detected during transmission. If the received CRC checksum matches the calculated CRC checksum for the original data, no errors occurred during transmission; otherwise, errors are detected.
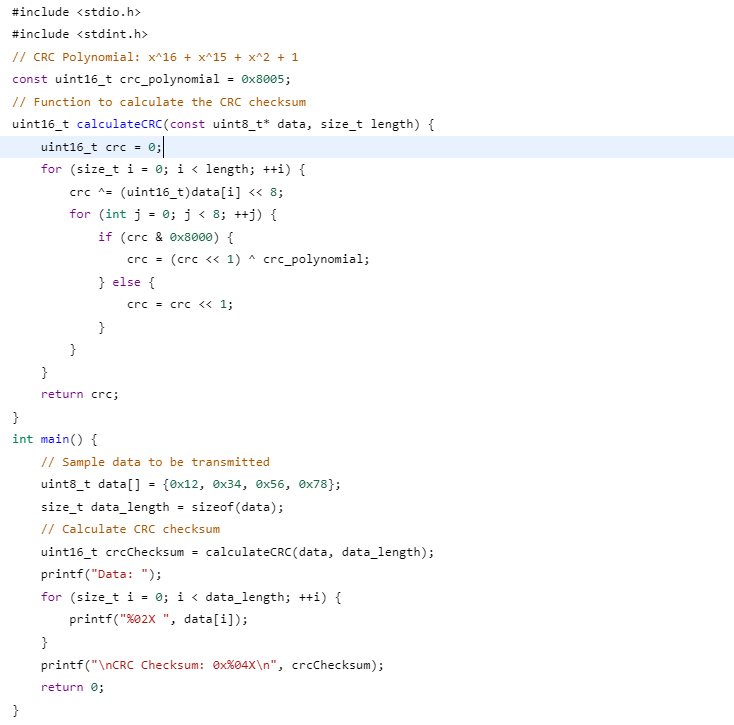
Here's a simple C program demonstrating the Cyclic Redundancy Check (CRC) algorithm for error detection. This example uses a common CRC polynomial, which is x^16 + x^15 + x^2 + 1 (expressed as 0x8005 in hexadecimal or 10000000000000011 in binary).
In this C program, the calculateCRC function calculates the CRC checksum for a given data array. The main function demonstrates how to use this function to calculate the CRC checksum for a sample data array (data) and then prints both the data and the resulting CRC checksum in hexadecimal format.
The Cyclic Redundancy Check (CRC) algorithm is primarily used for error detection, not error correction. When errors are detected using CRC, the usual practice is to request retransmission of the corrupted data or take corrective measures at the application level.
However, It's essential to understand that the CRC algorithm does not provide a way to fix or correct errors in the data. Instead, it serves as a mechanism to determine whether errors have occurred during transmission, allowing appropriate action to ensure data integrity.
The Cyclic Redundancy Check (CRC) algorithm is a robust and widely used error-detection technique, ensuring data integrity during transmission, storage, and retrieval processes. By appending a checksum to the data and comparing it at the receiving end, CRC detects errors and helps maintain the accuracy and reliability of the transmitted information. Understanding CRC's functioning and attributes is crucial for professionals in computer networking, data storage, and other fields relying on error-free data communication.
How does a Cyclic Redundancy Check (CRC) detect errors in data transmission?
CRC detects errors in data transmission by using a polynomial division algorithm. At the sender's end, the CRC algorithm calculates a checksum based on the data being transmitted and appends it to the data. The receiver independently calculates its own
CRC checksum for the received data. If both checksums match, the data is considered error-free. However, if the checksums differ, it indicates that errors have occurred during transmission, and the data integrity may be compromised.
How do I choose the appropriate CRC polynomial for my application?
Selecting the right CRC polynomial is crucial as it directly impacts the error-detection capabilities. The choice depends on factors such as the expected error rate, data length, and the types of errors to be detected. Commonly used CRC polynomials include CRC-16 (x^16 + x^15 + x^2 + 1), CRC-32 (Ethernet polynomial), and others. You can also use online tools or libraries that offer a range of CRC polynomials for specific applications.
How can CRC be applied to ensure data integrity in computer networks?
In computer networks, CRC is widely used in the Data Link Layer for error control. When transmitting data over the network, the sender calculates the CRC checksum and appends it to the data. Upon reception, the receiver recalculates the CRC checksum for the received data. If the calculated checksum matches the received one, it confirms error-free transmission. In cases of checksum mismatch, the receiver requests retransmission, ensuring reliable data transfer in network communication.
Leave a Reply
Your email address will not be published. Required fields are marked *