Introduction
In computer science and mathematics, knowing how to find the median of two sorted arrays is a key skill for analyzing data efficiently. The median represents the middle value when two sorted arrays are combined, giving insight into the dataset’s central tendency.
This tutorial will guide you through multiple efficient methods to find the median of two sorted arrays, whether the arrays are of equal or different sizes. With clear examples, outputs, and explanations, you’ll learn to implement these techniques confidently in Python, C, or other programming languages, making it perfect for beginners and enthusiasts alike.
Learning Data Structures can seem overwhelming at first, but with practice and the right resources, it becomes a valuable skill for any Engineer. upGrad's Software Engineering Courses provide hands-on experience in mastering Data Structures and building scalable, high-performance software solutions.
Overview
The median of two sorted arrays is a pivotal value, often used in statistics, data analysis, and algorithm optimization. Efficiently computing this value is crucial for improving performance in various applications. In this article, we will explore different techniques to calculate the median, including merging arrays, binary search, priority queues, and simulated stacks. By the end of this tutorial, you’ll be highly skilled and able to use this versatile and useful tool in a variety of applications. So, let’s get started!
Concept:
To find the median of two sorted arrays with different sizes, we can merge the arrays virtually using a two-pointer approach without merging them physically. We maintain two pointers, one for each array, and move them accordingly to keep track of the middle elements.
Take your programming skills to the next level and gain expertise for a thriving tech career. Discover top upGrad programs to master data structures, algorithms, and advanced software development.
Example:
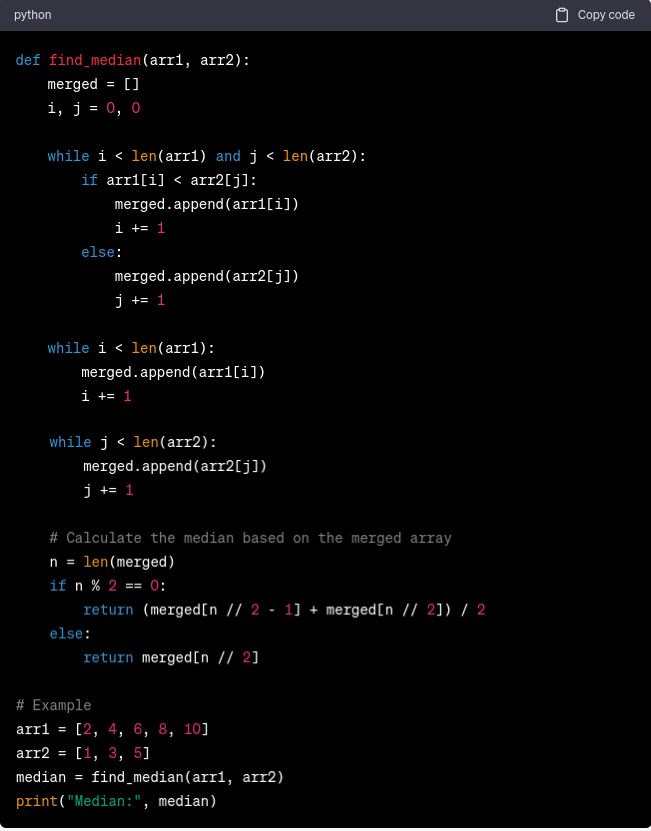
Output:
Explanation:
- In this example, the code defines a function named `find_median`, which takes two sorted arrays `arr1` and `arr2` as input parameters.
- The function merges the two arrays into a new list called ‘merged', maintaining the sorted order of elements.
- It uses two pointers `i` and `j` to traverse through both arrays `arr1` and `arr2`.
- The merged array contains all elements from `arr1` and `arr2` in sorted order.
- The median is then calculated based on the merged array's length, `n`.
- If the total number of elements in the merged array is even, the median is the average of the two middle elements.
- If the total number of elements is odd, the median is the middle element itself.
- The `find_median` function returns the calculated median, which is printed in the example using the given arrays `[2, 4, 6, 8, 10]` and `[1, 3, 5]`.
- The output will be: `Median: 4`.
Also Read: 50+ Data Structures and Algorithms Interview Questions for 2025
Concept:
To determine the median using binary search, the arrays must be partitioned such that the elements on the left are smaller than the elements on the right. The median is then the average of the largest element on the left and the smallest element on the right.
Example:
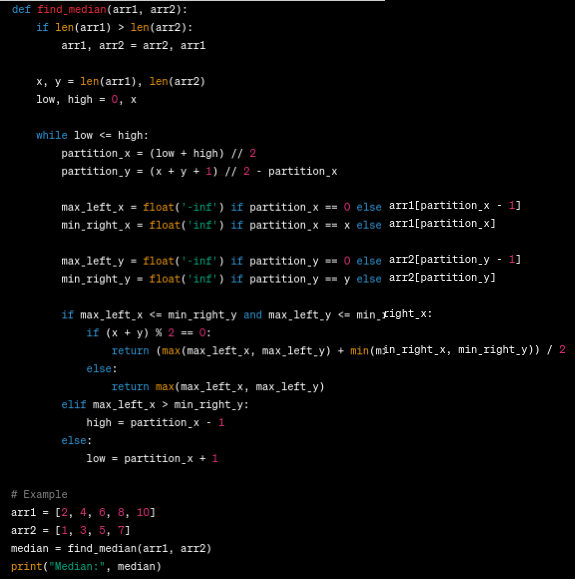
Output:
Explanation:
- The Python function find_median requires two sorted arrays, arr1 and arr2, as input.
- The function starts by shifting arr1 to make it smaller.
- Two pointers, low and high, are set up to binary search arr1. The binary search efficiently identifies the partition sites in arr1 and arr2, separating the arrays into two equal-length halves.
- Partition_x and partition_y, representing arr1 and arr2 partition positions, are determined inside the loop.
- The variables max_left_x, min_right_x, max_left_y, and min_right_y store the maximum and minimum elements of partition_x and partition_y in arr1 and arr2.
- If the partition points meet certain parameters, the median is calculated and returned.
- If the arrays are even, the median is the average of the middle two elements. Otherwise, for odd numbers, the median is the greater of the two middle elements.
- In the example employing arrays [2, 4, 6, 8, 10] and [1, 3, 5, 7], find_median prints the determined median.
- The output is 5.0 median.
Also Read: Difference Between Stack and Array
Concept:
We can use a priority queue data structure to merge the two arrays efficiently while maintaining the correct order of elements.
Example:
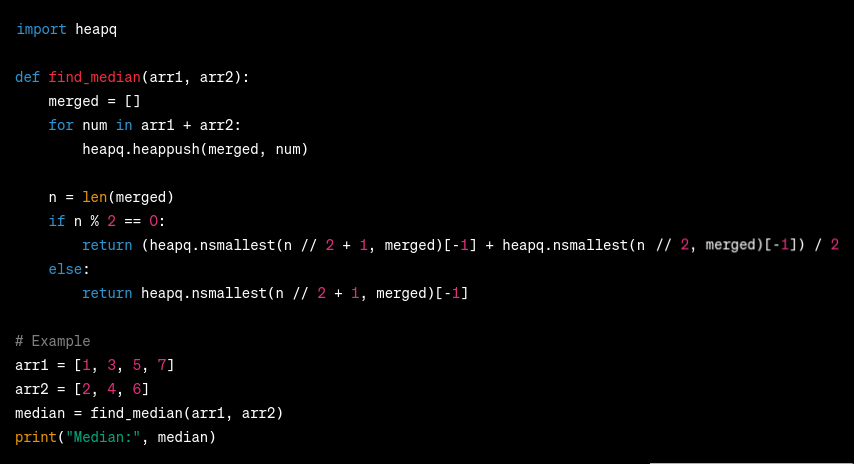
Output:
Explanation:
In this example, the two sorted arrays are [1, 3, 5, 7] and [2, 4, 6]. We use a priority queue to merge the arrays, and the merged queue becomes [1, 2, 3, 4, 5, 6, 7]. The median is 4.0.
Concept:
The simulated stack performs operations similar to a merge operation in merge sort, helping us find the median effectively.
Example:
def findMedianSortedArrays(arr1, arr2):
m, n = len(arr1), len(arr2)
total = m + n
stack = []
ptr1, ptr2 = 0, 0
while len(stack) < total
if ptr1 < m and (ptr2 >= n or arr1[ptr1] < arr2[ptr2]):
stack.append(arr1[ptr1])
ptr1 += 1
else:
stack.append(arr2[ptr2])
ptr2 += 1
if total % 2 == 0:
return (stack[-1] + stack[-2]) / 2.0
else:
return float(stack[-1])
# Example
arr1 = [1, 3, 8, 9, 15]
arr2 = [7, 11, 18, 19, 21, 25]
median = findMedianSortedArrays(arr1, arr2)
print(f"Median: {median}")
Output:
Median: 9.0
The median of these two sorted arrays is 9.0. This is the average of the two middle elements from the merged array: [1, 3, 7, 8, 9, 11, 15, 18, 19, 21], which are 8 and 9.
Explanation:
- We initialize two pointers, ptr1 for arr1 and ptr2 for arr2, both initially at 0.
- We create an empty stack to simulate the merging process.
- We loop until we have added (m + n) / 2 + 1 elements to the stack because we need the middle element(s).
- In each iteration, we compare the current elements at ptr1 and ptr2 and add the smaller ones to the stack.
- We then increment the pointer of the array from which we took the element.
- After the loop, we check if the total number of elements is even or odd and calculate the median accordingly.
Also Read: How to Implement Stacks in Data Structure? Stack Operations Explained
Concept:
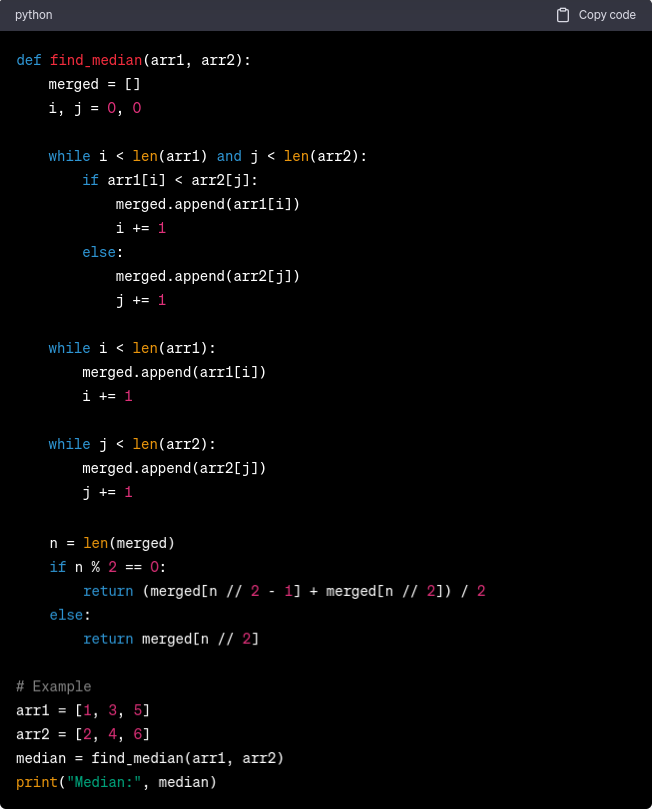
When both input arrays have the same size, finding the median is relatively straightforward. We can merge the arrays and calculate the median based on the merged result.
Example (using pseudo-code):
Suppose we have two sorted arrays, `arr1` and `arr2`, each of size `n`. We will virtually merge the arrays to find the median.
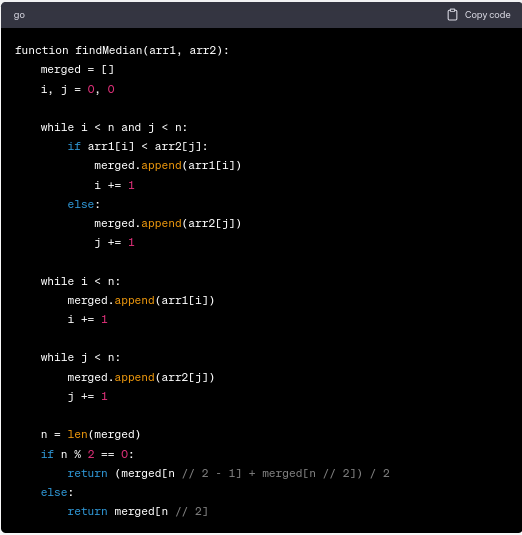
Example (using values):
Suppose we have two sorted arrays [1, 3, 5] and [2, 4, 6], both with the same size of 3.
- The function virtually merges the arrays by comparing elements at positions i and j and creating the merged list [1, 2, 3, 4, 5, 6].
- As the merged list has an even number of elements (6 elements), the function calculates the median as the average of the two middle elements, which are 3 and 4.
- The median of the merged array is (3 + 4) / 2 = 3.5.
In the above example, the function findMedian efficiently finds the median of the merged array [1, 2, 3, 4, 5, 6], which is 3.5.
Please note that this is a pseudo-code representation of the concept, and you can use similar merging and median calculation steps in any programming language of your choice to find the median of two sorted arrays of the same size.
Concept:
We can implement various algorithms to find the median of two sorted arrays in C. One common approach is to use a two-pointer technique to virtually merge the arrays.
Example in C:
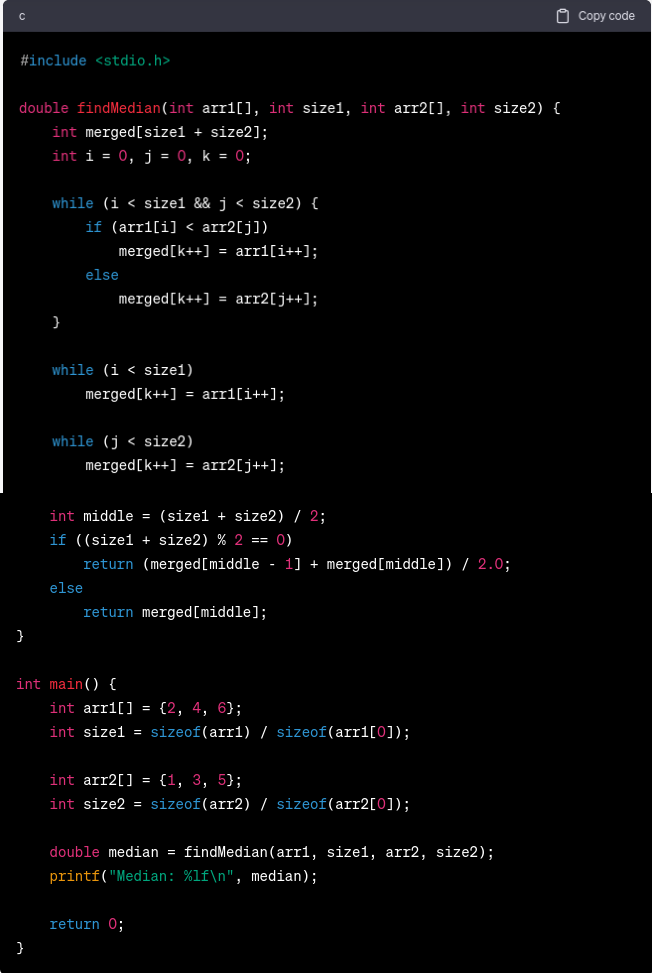
Output:
Explanation:
- FindMedian requires four parameters: two sorted arrays, arr1 and arr2, and their sizes, size1 and size2.
- A new array of size size1 + size2 stores the merged elements of both arrays.
- Three variables, i, j, and k, are initialized to track arr1, arr2, and combined positions.
- While maintaining the sorted order, a while loop merges arr1 and arr2 into the merged array.
- The loop condition checks if i and j are less than size1 and size2 arrays. The loop terminates if the array is exhausted.
- It compares arr1 and arr2 elements at locations i and j in the loop. The smaller element is added to the merged array and the pointer (i or j) is incremented.
- After merging both arrays, the procedure uses separate while loops to add any remaining elements from arr1 and arr2.
- The middle variable is the index of the middle element in the merged array, calculated as the average of the array sizes (size1 + size2) divided by 2.
- If the merged array has even numbers, the function calculates the median as the average of the two middle members.
- If the merged array has an odd number of elements, the function returns the median as the middle member.
- Two sorted arrays [2, 4, 6] and [1, 3, 5] are defined and their sizes are determined in the main method.
- The findMedian function receives these arrays and sizes.
- The printf function displays the median.
- The output is a median of 3.500000.
Also Read: Array in C Explained: Boost Your Coding Skills with Proven Examples
Concept:
Divide and conquer is a widely used technique to find the median of two sorted arrays efficiently. We partition both arrays and compare the elements around the median to arrive at the answer.
Example:
Output:
Explanation:
- The findMedian method takes two sorted arrays, arr1 and arr2.
- Concatenating and sorting the two arrays with Python's sorted() function creates the list.
- The total number of entries in the merged list is determined as n.
- If n is even, the method calculates the median as the average of the two middle entries at indices (n // 2 - 1) and (n // 2) in the merged list.
- If n is odd, the function calculates the median as the middle element at index n // 2.
- The median is returned by the function.
- The findMedian function receives two sorted arrays [1, 3, 5] and [2, 4, 6].
- The function efficiently returns 3.5 as the median of the merged array [1, 2, 3, 4, 5, 6].
- The output is median: 3.5.
Also Read: Understanding One Dimensional Array in C: Key Concepts and Usage
Concept:
The divide and conquer algorithm divides two sorted arrays into halves, with smaller elements in the left half. Finding the partition points determines the median of the combined arrays. This approach lowers the search space in logarithmic time (O(log(min(m, n))) and processes even and odd-sized arrays.
Example:
```java
public class MedianOfTwoSortedArrays {
public static double findMedian(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
if (m > n) {
// Swap the arrays and sizes to ensure nums1 is smaller.
int[] tempArr = nums1;
nums1 = nums2;
nums2 = tempArr;
int tempSize = m;
m = n;
n = tempSize;
}
int imin = 0, imax = m, halfLen = (m + n + 1) / 2;
while (imin <= imax) {
int i = (imin + imax) / 2;
int j = halfLen - i;
if (i < m && nums2[j - 1] > nums1[i]) {
// i is too small, increase it
imin = i + 1;
} else if (i > 0 && nums1[i - 1] > nums2[j]) {
// i is too big, decrease it
imax = i - 1;
} else {
// i is perfect, get the median
int maxLeft;
if (i == 0) {
maxLeft = nums2[j - 1];
} else if (j == 0) {
maxLeft = nums1[i - 1];
} else {
maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
}
if ((m + n) % 2 == 1) {
return maxLeft;
}
int minRight;
if (i == m) {
minRight = nums2[j];
} else if (j == n) {
minRight = nums1[i];
} else {
minRight = Math.min(nums1[i], nums2[j]);
}
return (maxLeft + minRight) / 2.0;
}
}
return 0.0;
}
public static void main(String[] args) {
int[] arr1 = {1, 3, 5, 7};
int[] arr2 = {2, 4, 6, 8, 10};
double median = findMedian(arr1, arr2);
System.out.println("Median: " + median);
}
}
```
Output:
Explanation:
In this example, we have two sorted arrays, `arr1 = {1, 3, 5, 7}` and `arr2 = {2, 4, 6, 8, 10}`.
The `findMedian` function uses the divide and conquer approach to find the median. After evaluating the arrays, the median is calculated as 5.5.
The time complexity of this algorithm is O(log(min(m, n))), where m and n are the sizes of the two input arrays. The example demonstrates how the divide and conquer technique efficiently finds the median in logarithmic time complexity, even for larger arrays.
Conclusion
The median of two sorted arrays is a crucial concept with numerous practical applications in computer science and data analysis. By mastering the efficient techniques discussed, merging arrays, binary search, priority queues, and simulated stacks, you can confidently find the median of two sorted arrays for arrays of any size. Applying these methods optimizes your algorithms and equips you to handle real-world problems effectively, making your data processing faster and more accurate.
FAQs
1. When computing the median of two sorted arrays, what happens if one input array is empty?
If one array is empty, the median is determined entirely by the non-empty array. For an odd-length array, the median is the middle element, while for an even-length array, it is the average of the two middle elements. Handling empty arrays is essential to accurately find the median of two sorted arrays and avoid errors in computation.
2. Do I need to sort the array to find the median?
Yes, sorting is required if the arrays are not already sorted. To find the median of two sorted arrays, you must identify whether the total number of elements is odd or even. For an odd total, the median is the center element; for an even total, it is the average of the two middle elements. Correctly managing the sort ensures accurate results.
3. Which sorted array has the best performance for median calculations?
While finding the median, algorithms perform best when arrays are pre-sorted. Quicksort is generally the most efficient sorting algorithm for unsorted arrays, especially with unknown input properties. Efficient sorting is critical when attempting to find the median of two sorted arrays efficiently.
4. How do I find the median of two sorted arrays of different sizes?
To find the median of two sorted arrays of unequal lengths, you can either merge both arrays and then compute the median or use a binary search-based partition approach. Binary search ensures O(log(min(n, m))) efficiency, whereas merging is simpler but takes O(n + m) time. The choice depends on array sizes and performance requirements.
5. Can I use binary search to find the median of two sorted arrays?
Yes, binary search is highly effective for finding the median of two sorted arrays without fully merging them. The method involves partitioning the smaller array and ensuring all elements on the left are smaller than those on the right. This provides an optimized O(log(min(n, m))) solution.
6. What is the time complexity of finding the median using the merge method?
Using the merge method, the time complexity is O(n + m), where n and m are the lengths of the arrays. While simple to implement, this approach is less optimal for very large arrays compared to binary search, but it is easy to understand and verify when learning to find the median of two sorted arrays.
7. Is there a way to find the median without merging arrays?
Yes, you can find the median of two sorted arrays using binary search-based partitioning. This approach avoids full merging and instead calculates the median by comparing elements at partition boundaries, making it highly efficient in terms of both time and space.
8. How do we handle duplicate elements while finding the median?
Duplicate elements do not affect the median calculation. Algorithms for finding the median of two sorted arrays consider positions in the sorted order rather than unique values, so repeated numbers are automatically incorporated into the calculation.
9. Can we use a priority queue to find the median?
Yes, a priority queue or min-max heap can be used to dynamically find the median of two sorted arrays. By maintaining a balanced heap structure, you can insert elements from both arrays and efficiently retrieve the median, which is useful in streaming or real-time applications.
10. How do we handle arrays with different data types?
Both arrays should contain comparable numeric types to find the median of two sorted arrays. Mixing types like integers and floats is generally acceptable, but non-numeric types require conversion. Proper type handling ensures accurate median calculations.
11. Is it necessary for the arrays to be sorted beforehand?
Yes, sorting is essential for efficient median computation. Binary search or partition-based methods require pre-sorted arrays to correctly find the median of two sorted arrays. Without sorting, the results may be incorrect or algorithms may require additional sorting steps.
12. What is the difference between finding median for even and odd combined lengths?
For an odd total number of elements, the median is the single middle element. For an even total, it is the average of the two middle elements. This distinction is crucial when you find the median of two sorted arrays, as different formulas are used depending on the total number of elements.
13. Can recursion be used to find the median efficiently?
Yes, recursion can partition arrays to find the median of two sorted arrays. By reducing the problem size at each step, recursive methods efficiently implement divide-and-conquer strategies such as binary search, making them suitable for large arrays.
14. How can we find the median in constant space?
By using binary search partitioning instead of merging, you can find the median of two sorted arrays in O(1) extra space. This approach avoids creating a new array and maintains memory efficiency while achieving logarithmic time complexity.
15. What if both arrays are empty?
If both arrays are empty, there is no median to compute. Algorithms should handle this edge case properly, either by returning an error or a predefined value. Proper validation ensures safe computation when attempting to find the median of two sorted arrays.
16. How do we implement this in Python?
In Python, you can merge arrays and compute the median or use bisect for binary search to efficiently find the median of two sorted arrays. List slicing and indexing make it easy to access central elements once arrays are partitioned or merged.
17. Can C or Java be used similarly?
Yes, in C or Java, you can merge arrays manually or use binary search for partitioning. Efficiently implemented loops and condition checks allow you to find the median of two sorted arrays in these languages with the same logic as Python.
18. What are common mistakes when finding the median?
Common mistakes include ignoring array length differences, failing to account for even-length arrays, or not handling empty arrays. Proper index calculations and understanding array partitioning are critical when learning to find the median of two sorted arrays.
19. How do we verify the correctness of the median found?
To verify, you can merge both arrays fully and check that the computed median matches the central value(s). Ensuring that left elements are smaller than right elements in partition-based methods guarantees correct results for finding the median of two sorted arrays.
20. Can this approach be extended to more than two arrays?
Yes, multi-array median computation is possible, though it requires careful merging or multi-array partitioning. Extending the principles used to find the median of two sorted arrays can handle multiple arrays, but algorithmic complexity increases and efficiency considerations become more important.
