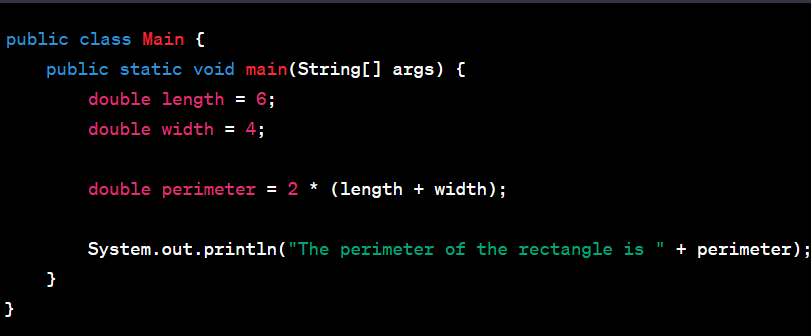
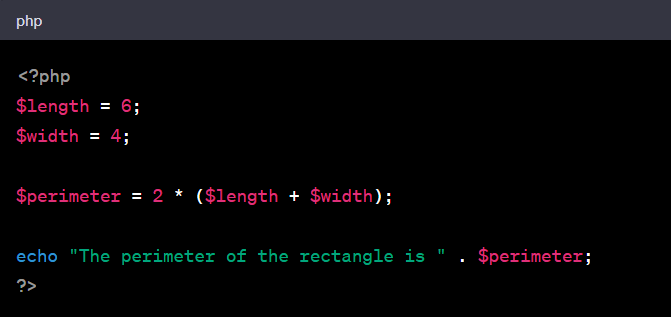
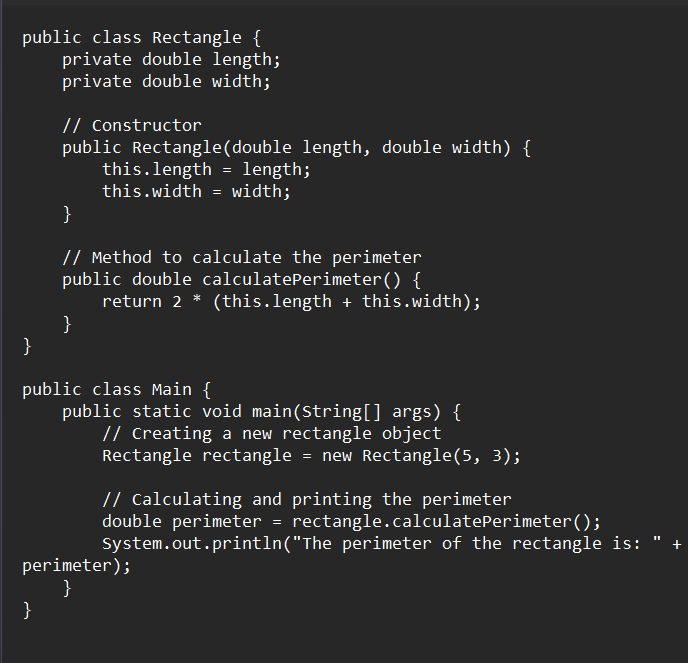
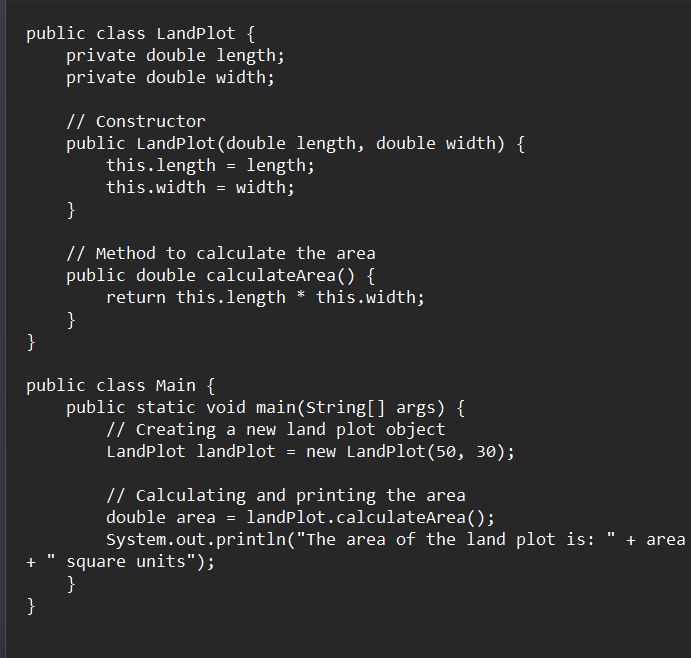
Working professionals
Domains
Doctorate
Artificial Intelligence
Machine Learning
Gen AI & Agentic AI
MBA
Marketing
Management
Education
Project Management
Data Science
Doctorate
For All Domains
IIITB & IIM, Udaipur
Chief Technology Officer & AI Leadership ProgrammeSwiss School of Business and Management
Global Doctor of Business Administration from SSBMEdgewood University
Doctorate in Business Administration by Edgewood UniversityGolden Gate University
Doctor of Business Administration From Golden Gate UniversityRushford Business School
Doctor of Business Administration from Rushford Business School, SwitzerlandGolden Gate University
Master + Doctor of Business Administration (MBA+DBA)Leadership / AI
Golden Gate University
DBA in Emerging Technologies with Concentration in Generative AIGolden Gate University
DBA in Digital Leadership from Golden Gate University, San FranciscoArtificial Intelligence
Degree / Exec. PG
IIIT Bangalore
Executive Diploma in Machine Learning and AIOPJ Global University
Master’s Degree in Artificial Intelligence and Data ScienceLiverpool John Moores University
Master of Science in Machine Learning & AIGolden Gate University
DBA in Emerging Technologies with Concentration in Generative AIExecutive Certificate
IIITB & IIM, Udaipur
Chief Technology Officer & AI Leadership ProgrammeIIIT Bangalore
Executive Programme in Generative AI for LeadersupGrad | Microsoft
Gen AI Foundations Certificate Program from MicrosoftupGrad | Microsoft
Gen AI Mastery Certificate for Data AnalysisupGrad | Microsoft
Gen AI Mastery Certificate for Software DevelopmentupGrad | Microsoft
Gen AI Mastery Certificate for Managerial ExcellenceOffline Bootcamps
upGrad
Data Science and AI-MLMachine Learning
Machine Learning
Gen AI & Agentic AI
Gen AI & Agentic AI
IIIT Bangalore
Executive Programme in Generative AI for LeadersMasters

Paris School of Business
Master of Science in Business Management and TechnologyO.P.Jindal Global University
MBA (with Career Acceleration Program by upGrad)Edgewood University
MBA from Edgewood UniversityO.P.Jindal Global University
MBA from O.P.Jindal Global UniversityGolden Gate University
Master + Doctor of Business Administration (MBA+DBA)Executive Certificate
IMT, Ghaziabad
Advanced General Management ProgramMarketing
Executive Certificate
upGrad | Microsoft
Gen AI Foundations Certificate Program from MicrosoftupGrad | Microsoft
Gen AI Mastery Certificate for Content CreationOffline Bootcamps
upGrad
Digital MarketingManagement
Degree
O.P Jindal Global University
MSc in International Accounting & Finance (ACCA integrated)
Paris School of Business
Master of Science in Business Management and TechnologyGolden Gate University
Master of Arts in Industrial-Organizational PsychologyExecutive Certificate
IIM Kozhikode
Human Resource Analytics Course from IIM-KupGrad | Microsoft
Gen AI Foundations Certificate Program from MicrosoftEducation
Education
Northeastern University
Master of Education (M.Ed.) from Northeastern UniversityEdgewood University
Doctor of Education (Ed.D.)Edgewood University
Master of Education (M.Ed.) from Edgewood UniversityProject Management
Certification
Knowledgehut
Leadership And Communications In ProjectsKnowledgehut
Microsoft Project 2007/2010Knowledgehut
Financial Management For Project ManagersKnowledgehut
Fundamentals of Earned Value Management (EVM)Knowledgehut
Fundamentals of Portfolio ManagementKnowledgehut
Fundamentals of Program Management-35c169da468a4cc481c6a8505a74826d.webp&w=128&q=75)
Knowledgehut
CAPM® CertificationsKnowledgehut
Microsoft® Project 2016Certifications & Trainings
-7f4b4f34e09d42bfa73b58f4a230cffa.webp&w=128&q=75)
Knowledgehut
PMP® Certification-7f4b4f34e09d42bfa73b58f4a230cffa.webp&w=128&q=75)
Knowledgehut
PMI-RMP® Certification-7f4b4f34e09d42bfa73b58f4a230cffa.webp&w=128&q=75)
Knowledgehut
PMP Renewal Learning PathKnowledgehut
Oracle Primavera P6 V18.8Knowledgehut
Microsoft® Project 2013-7f4b4f34e09d42bfa73b58f4a230cffa.webp&w=128&q=75)
Knowledgehut
PfMP® Certification CourseKnowledgehut
Project Planning and MonitoringPrince2 Certifications
Knowledgehut
PRINCE2® FoundationKnowledgehut
PRINCE2® PractitionerKnowledgehut
PRINCE2 Agile Foundation and PractitionerKnowledgehut
PRINCE2 Agile® Foundation CertificationKnowledgehut
PRINCE2 Agile® Practitioner CertificationManagement Certifications
-7f4b4f34e09d42bfa73b58f4a230cffa.webp&w=128&q=75)
Knowledgehut
Project Management Masters Certification ProgramKnowledgehut
Change ManagementKnowledgehut
Project Management TechniquesKnowledgehut
Product Management Certification ProgramKnowledgehut
Project Risk ManagementData Science
Degree / Exec. PG
O.P Jindal Global University
Master’s Degree in Artificial Intelligence and Data ScienceIIIT Bangalore
Executive Diploma in Data Science & AILiverpool John Moores University
Master of Science in Data ScienceExecutive Certificate
upGrad | Microsoft
Gen AI Foundations Certificate Program from MicrosoftupGrad | Microsoft
Gen AI Mastery Certificate for Data AnalysisupGrad | Microsoft
Gen AI Mastery Certificate for Software DevelopmentupGrad | Microsoft
Gen AI Mastery Certificate for Managerial ExcellenceupGrad | Microsoft
Gen AI Mastery Certificate for Content CreationOffline Bootcamps
upGrad
Data Science and AI-MLupGrad
Data AnalyticsFresh graduates
Domains
Data Science
Management
Marketing
Data Science
Bootcamp
Offline Bootcamps
upGrad
Data Science and AI-MLupGrad
Data AnalyticsManagement
Marketing
Bootcamp
upGrad Campus
Advanced Certificate in Performance MarketingOffline Bootcamps
upGrad
Digital Marketing- Study abroad
- Offline centres
More
RESOURCES
BlogsCutting-edge insights on education
WebinarsLive sessions with industry experts
TutorialsMaster skills with expert guidance
Learning GuideResources for learning and growth
COMPANY
Careers at upGradYour path to educational impact
Hire from upGradTop talent, ready to excel
upGrad for BusinessSkill. Shape. Scale.
Talent Hiring SolutionsReach. Rekrut. Redefine.
Experience centerImmersive learning hubs
About usOur vision for education
OTHERS
Refer and earnShare knowledge, get rewarded


Free Courses
Explore Our Free Software Tutorials

Free Certificate
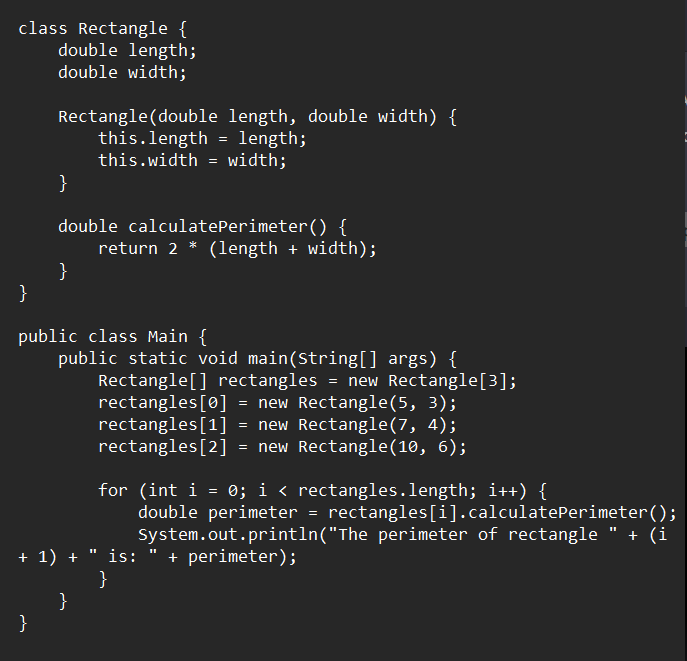
Object-Oriented Principles in Java
In this course, learn about the framework of classes and objects, and get introduced to the principles of OOP - Abstraction, Encapsulation, Inheritance and Polymorphism.
17 Courses

Free Certificate
Data Structures and Algorithm
This course focuses on building your problem-solving skills to ace your technical interviews and excel as a Software Engineer. In this course, you will learn time complexity analysis, basic data structures like Arrays, Queues, Stacks, and algorithms such as Sorting and Searching.
50 Courses

Free Certificate
Core Java Basics
In this course, you will learn the concept of variables and the various data types that exist in Java. You will get introduced to Conditional statements, Loops and Functions in Java.
17 Courses
upGrad Learner Support
Talk to our experts. We are available 7 days a week, 10 AM to 7 PM
Indian Nationals
Foreign Nationals
Disclaimer
The above statistics depend on various factors and individual results may vary. Past performance is no guarantee of future results.
The student assumes full responsibility for all expenses associated with visas, travel, & related costs. upGrad does not .










%20(1)-d5498f0f972b4c99be680c2ee3b792d7.svg)











-ae8d039bbd2a41318308f8d26b52ac8f.svg)