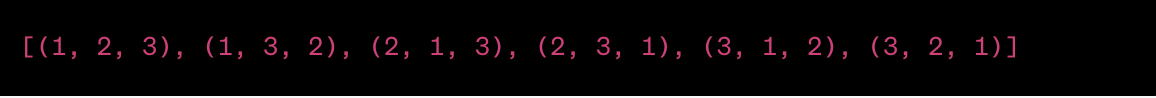Permutation and Combination in Python

Introduction

In the domain of computer science and programming, permutations constitute a fundamental concept. Python, a versatile programming language, equips us with powerful tools for handling permutations. This technical guide delves into the intricacies of permutations in Python, ranging from fundamental concepts to advanced methods. It focuses on generating permutations, combinations, and their associated variations, facilitating a deeper understanding of these critical combinatorial operations in Python.

Permutations play a pivotal role in computer science and programming, serving as the linchpin for a multitude of algorithms, including sorting, searching, and graph theory. In the Python programming environment, a profound understanding of permutations is indispensable for crafting efficient solutions to intricate problems. Furthermore, the significance of permutations extends into the realm of cryptography, where the secure generation of cryptographic keys and encryption techniques relies heavily on permutation-based operations. In the sphere of data analysis, permutations are harnessed for sampling and hypothesis testing, contributing to the development of statistically sound methodologies.

Combinatorial optimization, exemplified by problems like the traveling salesman dilemma and resource allocation, leans heavily on permutations as the cornerstone for finding optimal solutions, necessitating a deep comprehension of their properties. Within Python's versatile ecosystem, the itertools library provides a robust platform for generating permutations, combinations, and variations, accommodating a wide array of data types.

Overview

This comprehensive guide navigates the intricate world of permutations and combinations in Python, from their foundational principles to their diverse applications. It starts by introducing the essential itertools library for working with permutations and combinations. The guide then delves into permutations, offering insights into their mathematical underpinnings, Python implementation, and practical use cases. It further explores permutations with a fixed length, unveiling the flexibility of these combinatorial operations.

Moving on to combinations, the guide introduces their role in selecting elements without order considerations and discusses their relevance in mathematics and real-world scenarios. Special attention is given to combinations with replacement, a variant catering to specific use cases. Additionally, the blog demonstrates the application of permutations and combinations to strings and numeric sets and its use in text analysis, security, and more. This blog provides a comprehensive understanding of these concepts, real-world applications in data analysis, cryptography, combinatorial optimization, and their role in efficient problem-solving.

Importing the Required Library

Before we start generating permutations and combinations

• The necessary libraries have to be imported.
• This can be done in Python using the itertools library.

Here's how you can import it:

Permutation

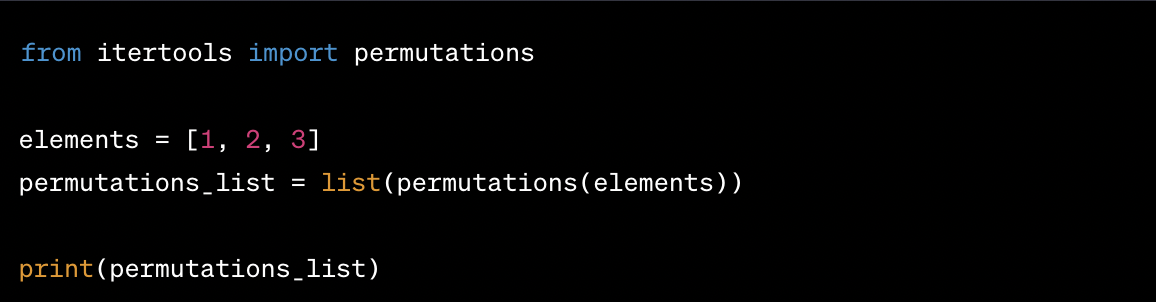
Generating permutations in Python uses the permutations function from the itertools library.

Example:

Output:

After running the code, you will get the following output:

In this example,

• The code generates all possible permutations of the elements [1, 2, 3].
• Each tuple in the output represents a unique permutation of the elements.
• As you can see, there are six different permutations, which is consistent with the mathematical concept of permutations for three distinct elements (3!).

Let us further explore this concept:

Permutations in Mathematics

In mathematics,

• a permutation is an arrangement of objects in a specific order. F
• or a set of n distinct objects, there are n! (n factorial) possible permutations.

The formula for calculating permutations is:

a. Permutations in Python

• Python's permutations function is part of the itertools library.
• It generates all possible permutations of a given iterable.
• The input iterable can contain elements of any data type.

For example, if you have a list of elements:

You can find all the permutations of this list using the permutations function:

The code above will output a list of tuples, where each tuple represents a unique permutation.

In this case, it will yield the following permutations:

There are six permutations, as there are three elements, and the formula 3! gives us six possibilities.

b. Permutation of Fixed Length

Let us see how you can specify the length as an argument to the permutations function. This is useful when you need permutations of a fixed length in this manner:

The permutations_list = list(permutations(elements, 2)) code will generate permutations of length 2 from the given elements.

c. Applications of Permutations

Permutations have practical applications such as:

1. Passwords

In cybersecurity, password permutations enhance security by generating and testing various password combinations. By considering all possible permutations of characters, you can strengthen your passwords.

2. Cryptography

Permutations are a fundamental part of encryption algorithms. Permuting data or keys helps protect information from unauthorized access.

3. Game Development

In game development, permutations are used for generating different combinations of game elements, such as puzzles or character movements.

4. Data Analysis

Permutations are applied in data analysis and statistics to explore all possible arrangements of data and make informed decisions.

You can unlock numerous possibilities in these and other areas by understanding permutations.

Combination

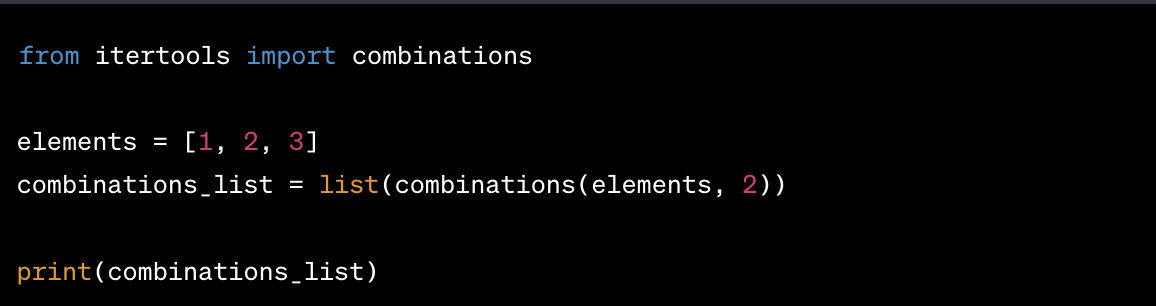
Python's combinations function from the itertools library is your tool for combination, which refers to selecting elements from a set without regard to the order.

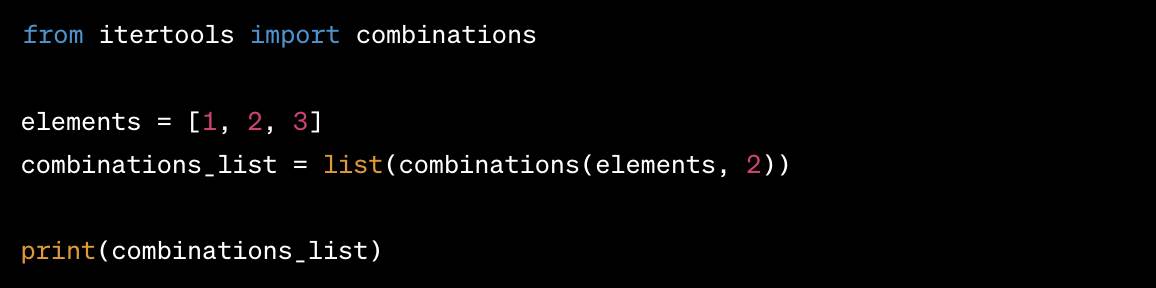
Example:

combinations_list = list(combinations(elements, 2)) will provide all the possible combinations of 2 elements from the set [1, 2, 3].

Here are some practical applications of Combinations:

a. Combinations in Mathematics

In mathematics, combinations represent the selection of items from a larger pool, regardless of the order in which they are selected. The number of combinations of n items taken r at a time is calculated using the binomial coefficient formula:

b. Combinations in Python

Python's itertools library provides the combinations function,

• making it easy to generate combinations of elements from an iterable.
• This function returns an iterator, which can be converted to a list for further use.

For example, if you have a list of elements:

You can find all the combinations of 2 elements from this list using the combinations function:

The code above will output a list of tuples, where each tuple represents a unique combination of 2 elements:

In this case, it will yield three combinations.

c. Applications of Combinations

Combinations are widely used in various fields due to their ability to represent selections and possibilities. Here are a few practical applications of combinations:

1. Lottery Numbers

In lotteries and games of chance, combinations are used to determine the winning numbers. Players select a specific combination of numbers, and the drawn numbers are compared to these combinations to determine winners.

2. Team Selection

In sports and competitions, combinations are employed to choose teams from a pool of players. The order of selection doesn't matter in such cases.

3. Combinatorial Analysis

Combinatorial analysis involves counting and analyzing the possible combinations of elements in different scenarios, such as the arrangement of cards in a deck.

4. Genetics

In genetics and biology, combinations play a role in the distribution of genes and traits from parents to offspring.

d. Combination of Strings

Combinations can be applied to strings as well.

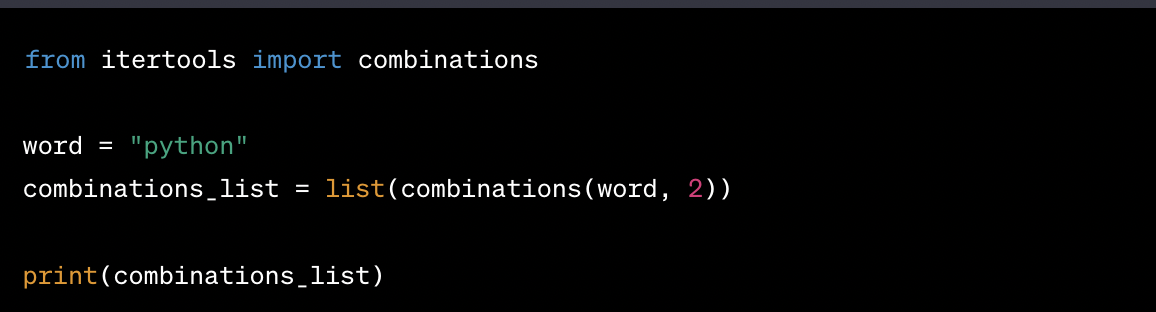
Example: To find all possible two-letter combinations of a word, Python can handle that too.

Here's an example:

This code will generate all the two-letter combinations from the string "python."

e. Exploring String Combinations

Working with combinations of strings can be particularly useful in various applications, including:

1. Text Analysis

Examining combinations of letters or words in text analysis can help identify patterns, anagrams, and potential linguistic insights.

2. Password Cracking

Security experts and hackers use combinations of letters and numbers to attempt to crack passwords or encryption keys.

3. Cryptanalysis

In cryptography, analyzing combinations of characters in encrypted messages can provide clues for breaking codes and ciphers.

4. Language Processing

In natural language processing, exploring combinations of words or phrases can help build language models, improve machine translation, and enhance chatbots and virtual assistants.

f. Combination with Replacement

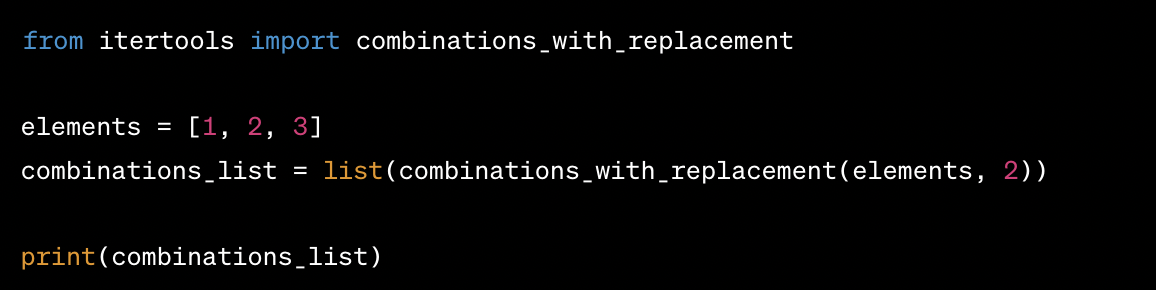
In some scenarios, you might want to allow elements to be combined more than once. Python's combinations_with_replacement function is designed for this purpose.

Here's an example:

This code will provide all the combinations of 2 elements from the set [1, 2, 3], with replacement.

g. Understanding Combinations with Replacement

Combinations with replacement are applicable in various practical scenarios:

1. Probability and Statistics

In probability and statistics, combinations with replacement are used to calculate the likelihood of events, such as drawing cards from a deck or rolling dice.

2. Sampling

In sampling and data analysis, combinations with replacement can help simulate the random selection of items from a population.

3. Experimental Design

In experimental design, researchers use combinations with replacements to generate test cases, assess the impact of variables, and plan experiments.

h. Combination of Numeric Sets

Working with numeric sets requires specific techniques. Python's combinations and combinations_with_replacement functions can be used to tackle numeric combinations effectively. We'll provide an in-depth explanation and examples.

Generating Combinations of Numeric Sets

When working with numeric sets, you can use Python's itertools library to generate combinations. The process is similar to what we've seen with strings and other data types.

Let's take a look at an example:

This code will produce all possible combinations of 3 elements from the numeric set [1, 2, 3, 4].

Conclusion

In this guide, we've explored permutations and combinations in Python. We've covered the essential topics and provided code examples. Some key learnings from this module include:

• Comprehensive Understanding: This guide has provided a comprehensive understanding of permutations and combinations in Python, leveraging the itertools library.
• Key Mathematical Concepts: We've explored key mathematical concepts behind permutations and combinations.
• Real-World Applications: These concepts find applications in numerous real-world scenarios, from cybersecurity (password generation) to statistical analysis (hypothesis testing).
• Computational Complexity: It's crucial to be mindful of the computational complexity, primarily determined by the size of the input iterable when generating permutations and combinations.
• Coding Proficiency: Readers are now equipped with the proficiency to write Python code for permutations and combinations, enabling them to tackle a wide range of combinatorial challenges in their programming projects.
• Versatility: The itertools library's versatility allows for permutations and combinations of elements in any data type, including strings with special characters and spaces.
• Problem Solving: The understanding of permutations and combinations extends beyond theoretical concepts, enabling efficient problem-solving in practical domains like cryptography, game development, and data analysis.

FAQs

1: What is itertools in Python?

The primary library for working with permutations and combinations in Python is itertools. It provides functions like permutations, combinations, and combinations_with_replacement for these tasks.

2: What is the difference between combinations and combinations with replacement?

Combinations involve selecting elements from a set without replacement, meaning each element can only be chosen once. Combinations with replacement allow elements to be selected more than once.

3: Are there any practical applications of permutations and combinations in real-world programming or data analysis?

Yes, permutations and combinations have numerous practical applications.

• In data analysis, they are used for statistical sampling and hypothesis testing.
• In cryptography, they play a role in encryption and decryption algorithms.
• In combinatorial optimization problem scenarios like password generation and game development.

4: Are there Python libraries or tools other than itertools for working with permutations and combinations?

While itertools is a primary library for handling permutations and combinations in Python, there are other third-party libraries available, such as 'more-itertools' and 'sympy,' that offer additional features and functionality for combinatorial tasks. These libraries can be explored to meet specific requirements in certain scenarios.