Program for Linear Search in C: Step-by-Step Code and Logic

How do you find an item in an unsorted array without sorting it first?

You write a program for linear search in C—the simplest search algorithm.

A program for linear search in C goes through each element in an array one by one until it finds the target value or reaches the end. It’s easy to implement and works well for small or unsorted datasets. If you're just starting with C programming, linear search is one of the best examples to practice loops, arrays, and conditional logic.

In this tutorial, you’ll learn how to write a program for linear search in C with and without user input. We’ll break down the logic, explain the search process, and show how to return the element’s index—or indicate that it wasn’t found.

By the end, you'll have a working program and a solid understanding of linear search basics. Want to strengthen your programming fundamentals? Check out our Software Engineering Courses to build real-world coding skills.

Understanding Linear Search

Linear search algorithm sequentially compares each element in a list to the target. It’s a basic approach useful for small datasets, such as searching for a contact in a phonebook, verifying user credentials in a system, or finding a specific item in a warehouse inventory.

The idea behind it is straightforward:

• Start at the first element of the list (index 0).
• Compare each element with the target value (key).
• If a match is found, return the index of that element.
• If the target is not found after checking all elements, return "not found" or an indicator like -1.

Let’s use an example to understand these steps:

Input:

• Array: {10, 50, 30, 70, 80, 60, 20, 90, 40}
• Key (target): 30

Process:

• Start at index 0: Compare 10 with 30. Not a match.

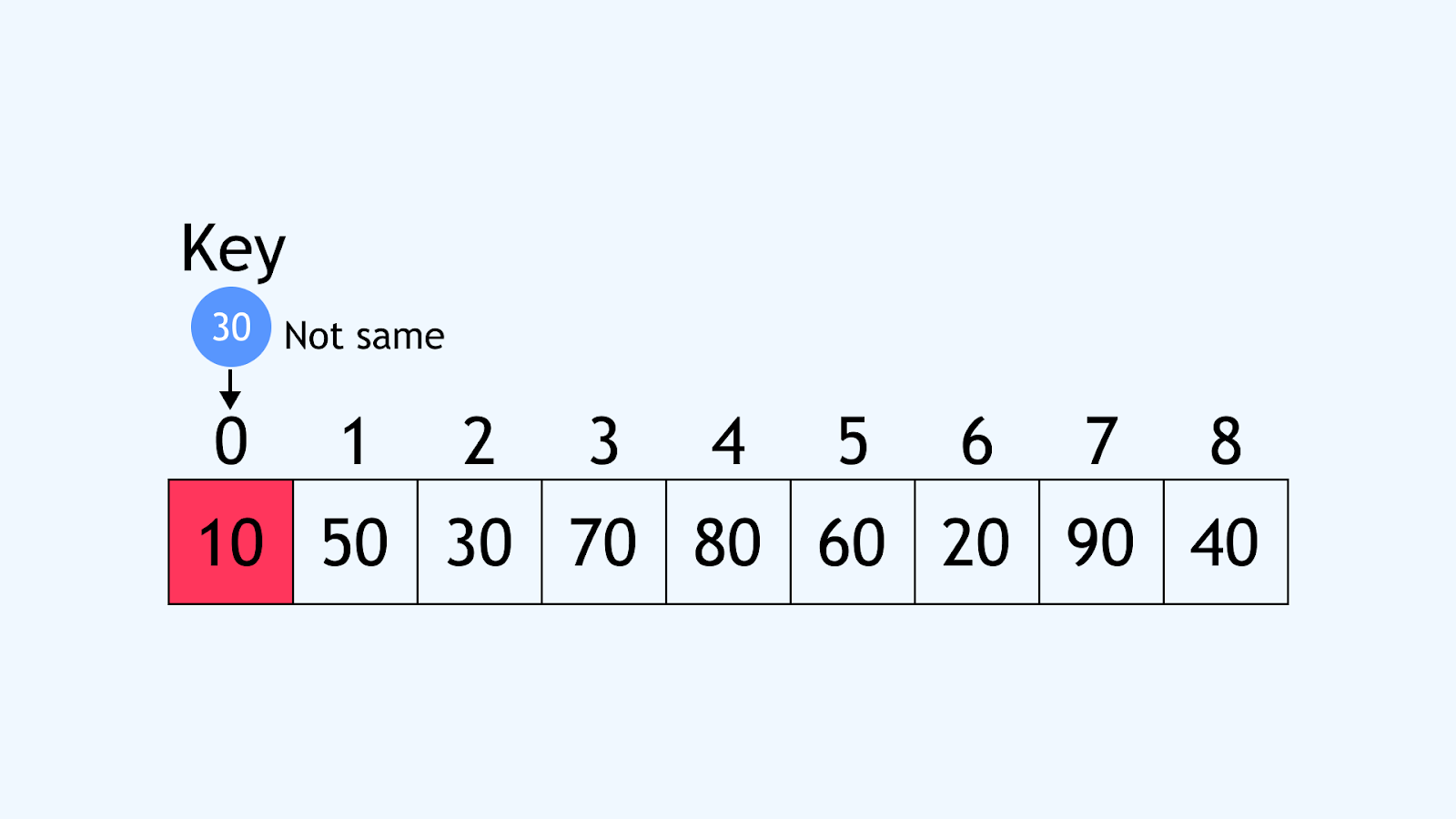
• Move to index 1: Compare 50 with 30. Not a match.

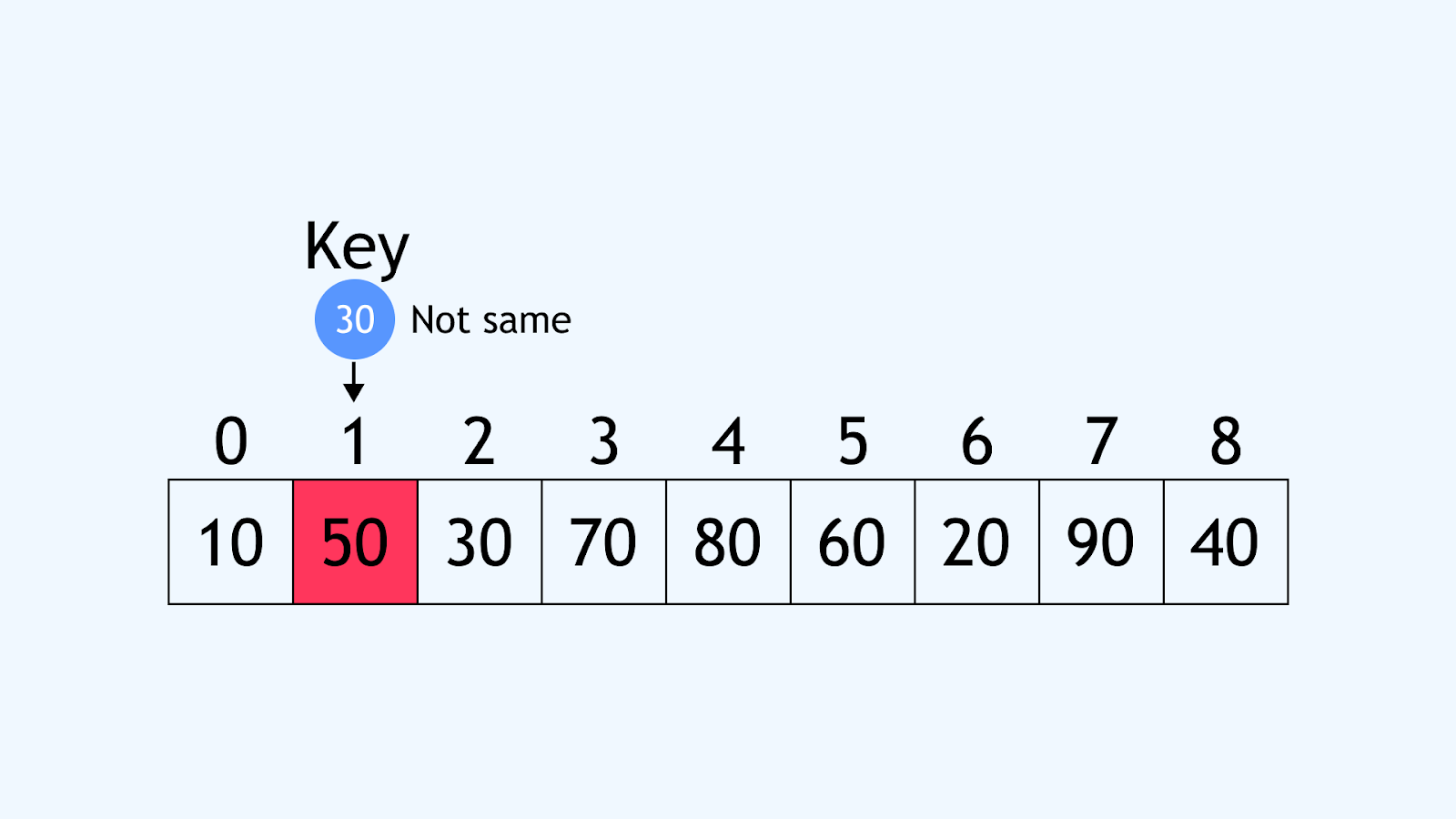
• Move to index 2: Compare 30 with 30. Match found!

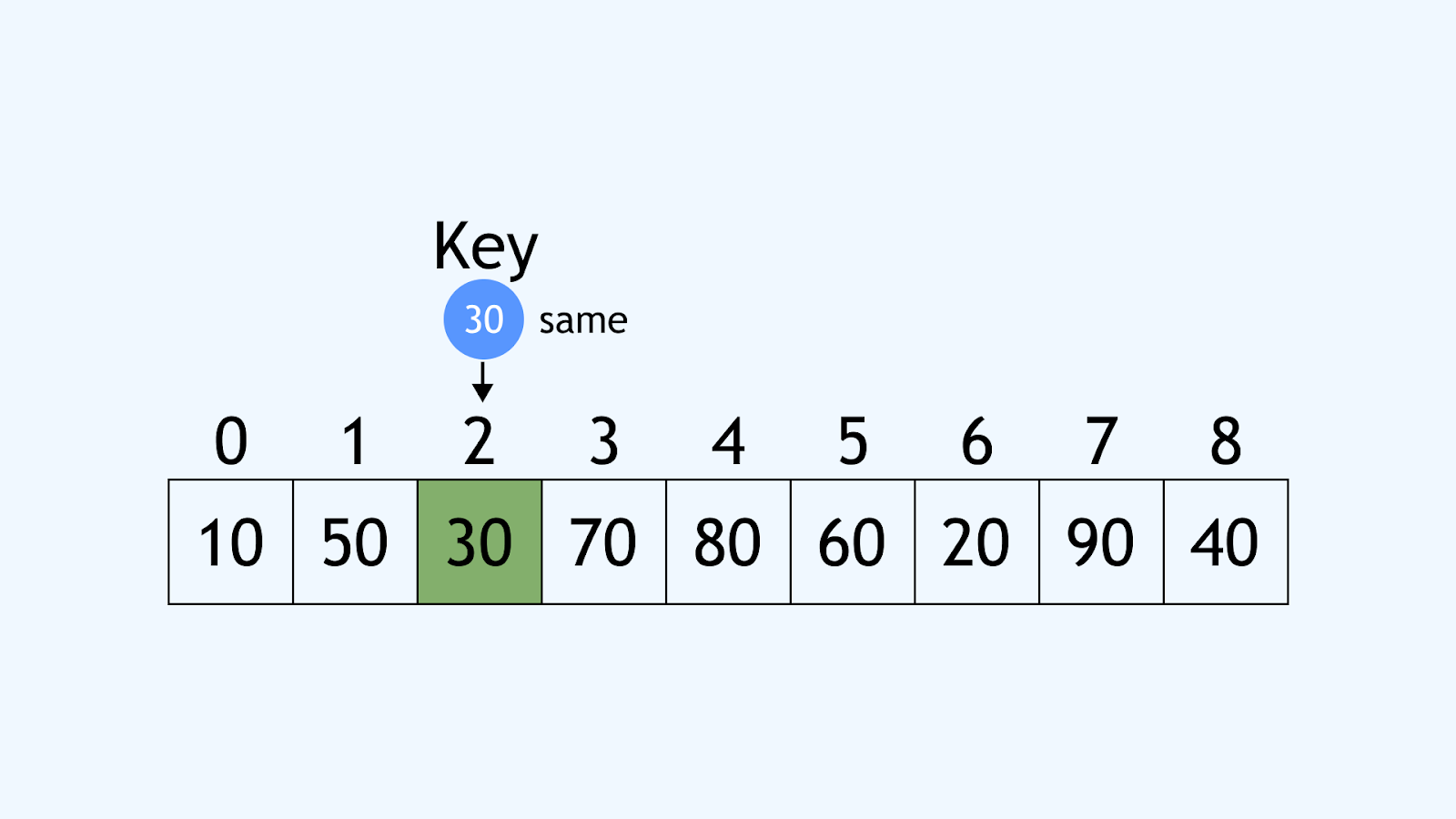
Output: Key found at Index 2

Explanation: The algorithm starts from index 0 and checks each element in the list. When it reaches index 2, the value 30 matches the target value (key), and it stops. It then returns the index (2) where the element was found.

Also Read: Difference Between Linear Search and Binary Search

With the basic understanding of linear search in place, let’s now look at how to implement it in C using a simple function.

Ready to move beyond C programming and unlock new career opportunities? We've curated these forward-looking courses specifically to enhance your professional growth:

• Professional Certificate Program in Cloud Computing and DevOps
• AI-Powered Full Stack Development Course by IIITB
• Future-Proof Your Tech Career with AI-Driven Full-Stack Development

Program for Linear Search in C Using a Function

A linear search algorithm in C is used to find an element in an array. C is often used for this algorithm due to its low-level control over memory and efficient handling of arrays.

Unlike higher-level languages, C allows direct memory access and optimized performance for tasks like linear search, making it ideal for simple search operations in small to medium-sized datasets.

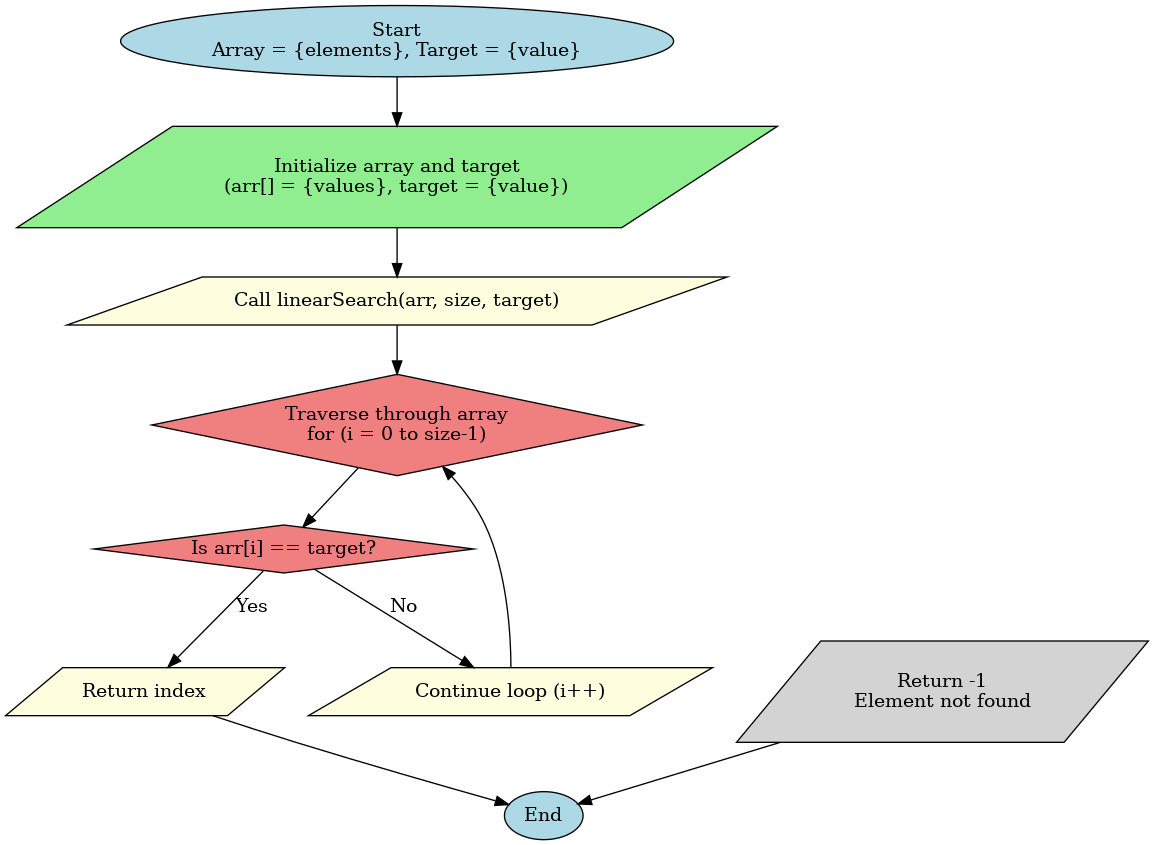
Here's a program for linear search in C using a function:

#include <stdio.h>
// Function to perform linear search
int linearSearch(int arr[], int n, int target) {
// Traverse through the array
for (int i = 0; i < n; i++) {
// If the target element is found, return its index
if (arr[i] == target) {
return i;
}
}
// If the target element is not found, return -1
return -1;
}
int main() {
int arr[] = {5, 9, 3, 7, 2};  // Array to search in
int size = sizeof(arr) / sizeof(arr[0]);  // Calculate the size of the array
int target = 7;  // Element to search for
// Call the linearSearch function
int result = linearSearch(arr, size, target);
// Check if the element was found and print the result
if (result == -1) {
printf("Element not found\n");
} else {
printf("Element found at index %d\n", result);
}
return 0;
}

Explanation:

1. The linearSearch function takes three arguments:

• arr[]: the array to search.
• n: the size of the array.
• target: the element we're looking for.

2. The function loops through each element of the array:

• If it finds the target element, it returns the index of that element.
• If the element is not found after checking the entire array, it returns -1.

3. In the main function:

• You declare an array arr[] with some numbers.
• You calculate the size of the array using sizeof(arr) / sizeof(arr[0]).
• You set the target element to search for, which is 7 in this example.

4. Then, you call the linearSearch function to search for the target in the array.Finally, you print the result. If the target is found, you display its index; if not, you display "Element not found".

Output:

Element found at index 3

This output shows that the target element 7 was found at index 3 in the array.

Also Read: Top 25+ C Programming Projects for Beginners and Professionals

Now that you have the basic implementation, let's see how you can extend this to find multiple occurrences of an element within the array.

Linear Search for Multiple Occurrences in C

In certain scenarios, you might need to find all occurrences of a specific element in an array. The code below performs a linear search and prints all indices where the target element is found, along with the total number of occurrences.

Here's an example of a program for linear search in C with multiple occurrences:

#include <stdio.h>
void linearSearchMultipleOccurrences(int arr[], int n, int key) {
int count = 0;
printf("Occurrences of key %d found at indices: ", key);
// Traverse the array and check each element
for (int i = 0; i < n; i++) {
if (arr[i] == key) {
printf("%d ", i);  // Print index of element
count++;            // Increment the count of occurrences
}
}
// If no occurrence is found
if (count == 0) {
printf("Element not found.");
} else {
printf("\nTotal occurrences: %d", count);
}
}
int main() {
int arr[] = { 10, 50, 30, 70, 30, 60, 30, 90, 40 };
int n = sizeof(arr) / sizeof(arr[0]);
int key = 30;
// Calling linearSearchMultipleOccurrences function
linearSearchMultipleOccurrences(arr, n, key);
return 0;
}

Explanation:

1. Function (linearSearchMultipleOccurrences): The function takes three parameters: the array arr[], its size n, and the target key to search for.

• It iterates through the array and checks if the current element matches the target.
• For each match, it prints the index and increments a counter to track the total number of occurrences.

2. Count and Output: If no occurrences are found, the function prints "Element not found". Otherwise, it prints all the indices where the target is found and the total number of times the element appears in the array.

Output:

Occurrences of key 30 found at indices: 2 4 6

Total occurrences: 3

This output shows that the target element (30) was found at indices 2, 4, and 6 in the array, and it appears 3 times. This program for linear search in C efficiently handles multiple occurrences in the dataset.

Also Read: Difference Between C and Java: Which One Should You Learn?

Having covered multiple occurrences, let’s take a deeper dive into pointer-based linear search, which offers more control over memory.

Linear Search Function Using Pointers

Linear search using pointers in C directly accesses array elements via pointer arithmetic (arr++), which moves the pointer to the next element in the array. Initially, the pointer points to the first element, and after each comparison, arr++ increments the pointer to the next element.

This allows the search to continue through the array until the target is found or the end of the array is reached. Unlike the index-based approach, which uses arr[i], the pointer method can be more memory-efficient and is especially useful for larger datasets.

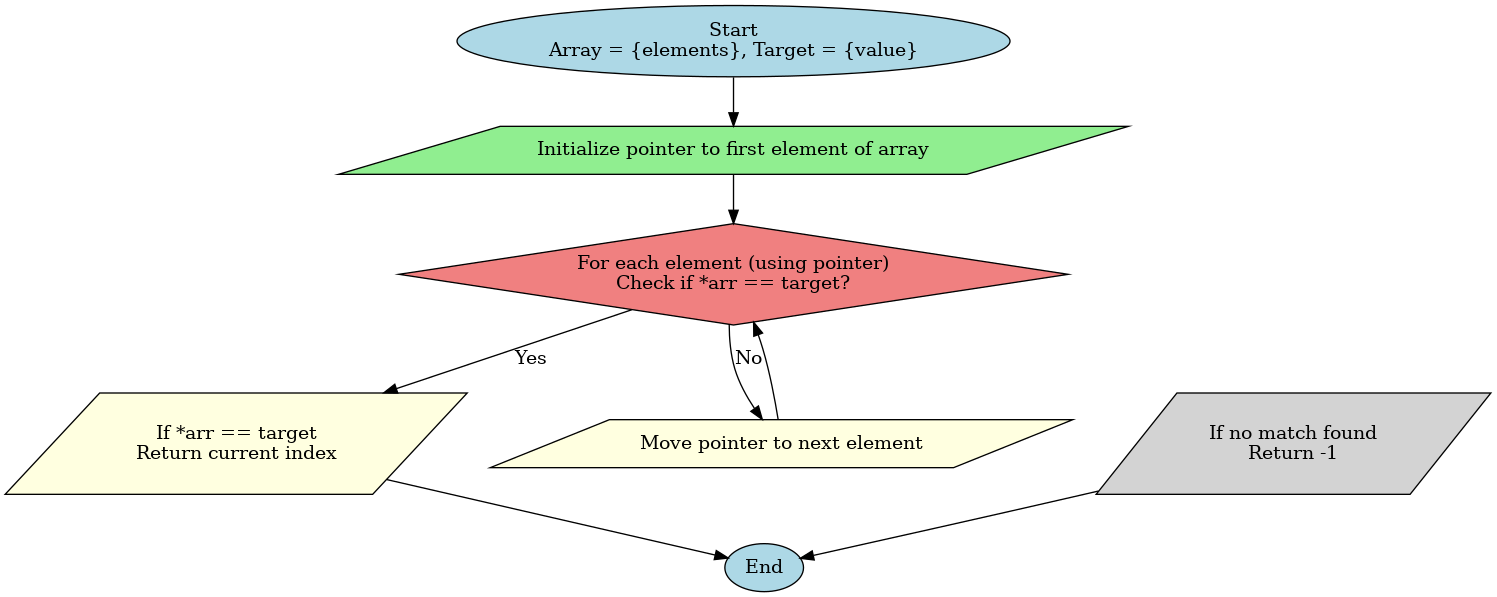
Here's an example of a program for linear search in C that uses a function with pointers:

#include <stdio.h>
// Function to perform linear search using pointers
int linearSearch(int *arr, int size, int target) {
// Traverse the array using pointer arithmetic
for (int i = 0; i < size; i++) {
// If the target element is found, return its index
if (*arr == target) {
return i;
}
arr++;  // Move the pointer to the next element
}
// If the target element is not found, return -1
return -1;
}
int main() {
int arr[] = {5, 9, 3, 7, 2};  // Array to search in
int size = sizeof(arr) / sizeof(arr[0]);  // Calculate size of the array
int target = 7;  // Element to search for
// Perform linear search using pointer-based function
int result = linearSearch(arr, size, target);
// Check if the element was found and print the result
if (result == -1) {
printf("Element not found\n");
} else {
printf("Element found at index %d\n", result);
}
return 0;
}

Explanation:

1. When using linearSearch function (Using Pointers):

• The function accepts a pointer arr to the array, the size of the array, and the target element to search for.
• It uses pointer arithmetic to traverse the array. arr++ increments the pointer to move to the next element.
• If the target element is found (*arr == target), it returns the index of that element.
• If the target is not found after checking the entire array, it returns -1.

2. When using the main function:

• We declare an array arr[], calculate its size, and specify the target element to search for (7 in this case).
• The linearSearch function is called, and the result is checked to see if the element was found or not.
• If found, it prints the index; otherwise, it prints "Element not found".

Output:

Element found at index 3

This output shows that the target element 7 was found at index 3 in the array. Using pointers with the linear search algorithm in C allows direct access to array elements and provides an efficient way to iterate through them.

Also Read: Data Types in C and C++ Explained for Beginners

Next, you will explore how to implement linear search using recursion, which provides an alternative to the traditional iterative approach.

Recursive Implementation of Linear Search in C

In recursive linear search, each recursive call reduces the problem size by checking one element at a time and then calling the function again with a smaller array (decreasing the size n).

The stack unwinds as each call finishes, returning either the index of the element (if found) or -1 (if not found). Tail recursion can optimize this process, where the recursive call is the last operation in the function.

It potentially reduces memory overhead and improves performance, although it doesn't always match the efficiency of the iterative approach in C.

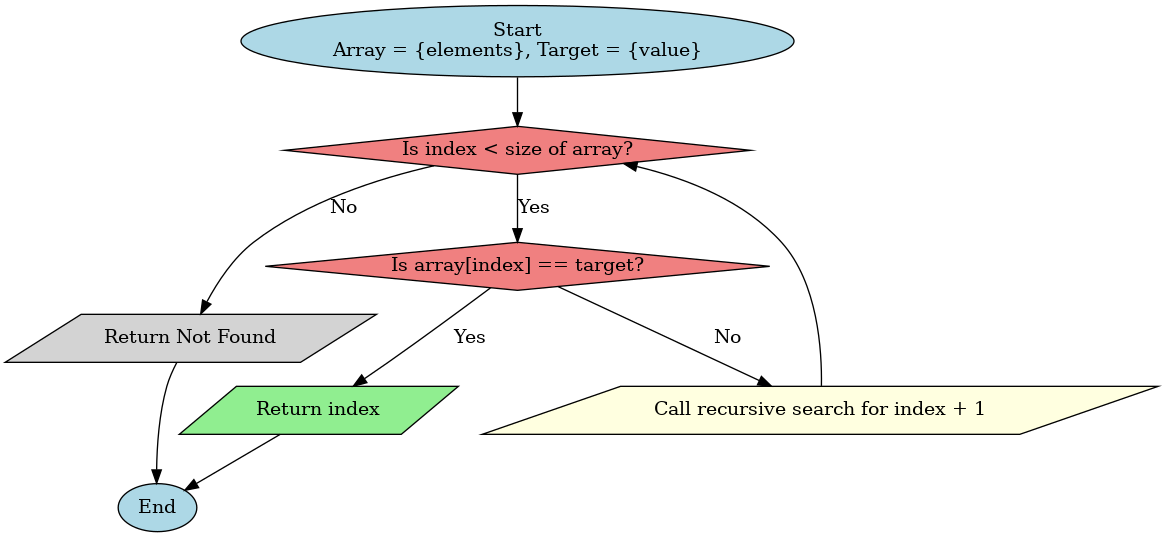
Here's an example of a program for linear search in C using recursive method:

// C Program to implement linear search using recursion
#include <stdio.h>
int linearSearch(int* arr, int n, int key) {
// Base Case: if there are no elements, return -1
if (n == 0)
return -1;
// If the element at (n - 1) index is equal to key, return (n - 1)
if (arr[n - 1] == key) {
return n - 1;
}
// If element is not at n - 1, call linearSearch for the same array but reducing the size by a single element
// Recursive function reducing array size at each call
return linearSearch(arr, n - 1, key);
}
int main() {
int arr[] = { 10, 50, 30, 70, 80, 60, 20, 90, 40 };
int n = sizeof(arr) / sizeof(int);
int key = 30;
// Calling linearSearch function
int i = linearSearch(arr, n, key);
if (i == -1)
printf("Key Not Found");
else
printf("Key Found at Index: %d", i);
return 0;
}

Explanation:

1. Recursive Function (linearSearch): This function works by checking the last element of the array (arr[n-1]) against the target key.

• If a match is found, it returns the index of the element.
• If no match is found, the function calls itself with a reduced array size (n-1).
• The recursion continues until the base case (n == 0) is reached, indicating that the element was not found.

2. Base Case: When the size (n) becomes 0, the function returns -1, indicating that the element isn't in the array.

3. Recursive Case: The function checks the current last element, and if it doesn't match the target, it makes a recursive call to search the rest of the array.

Output:

Key Found at Index: 2

This output shows that the target element (30) was found at index 2 of the array. The recursive implementation allows you to explore the array in a step-by-step manner, utilizing the call stack for the search process.

Also Read: What Are Storage Classes in C?

After understanding the recursive approach, let’s explore how linear search handles edge cases.

Handling Edge Cases in Linear Search

Before starting the search, ensure the array is not empty. If the array is empty, the search should immediately return -1, indicating that the element is not found. Additionally, when searching for an element at the first or last index of the array, keep in mind that:

• If the element is at the first index, it will be found immediately.
• If the element is at the last index, the search will need to check all elements before finding the match.

So, in the worst-case scenario, if the target is at the last index, the algorithm will traverse the entire array before identifying the target.

Once you’ve grasped different types of linear search implementations, let's shift focus to the complexity analysis to evaluate the efficiency of the linear search algorithm.

Complexity Analysis of Linear Search

Complexity analysis helps us understand how linear search performs as the input size increases. It shows how the number of comparisons grows, helping us assess the algorithm's efficiency in different scenarios.

Time complexity explains how quickly the search finishes.

• Best case (O(1)): If the target element is found at the first position, only one comparison is needed.
• Worst case (O(n)): If the target element is not in the array, we must compare it with every element, making n comparisons (where n is the array size).
• Average case (O(n)): On average, we make about n/2 comparisons, so the time complexity is still O(n).

Also Read: Why Is Time Complexity Important: Algorithms, Types & Comparison

Space complexity tells us how much memory the algorithm needs.

• O(1): Linear search uses a constant amount of space, as it only requires space for variables and does not depend on the input size.

In summary, linear search has linear time complexity (O(n)) and constant space complexity (O(1)).

While this makes it simple and effective for small or unsorted datasets, it's not the most efficient choice for larger datasets. Let’s compare linear search with Binary Search and Hashing, which offer better performance for sorted and large datasets.

Here’s a comparison table:

Also Read: Time and Space Complexity in Machine Learning Explained

Now that you’ve analyzed its complexity, let’s explore the advantages and disadvantages of linear search, so you can better assess when to use it.

Advantages and Disadvantages of Linear Search

Linear search is a simple and versatile algorithm used to find an element in a data structure. It is easy to implement and can be used with both sorted and unsorted data, making it useful in many scenarios. However, its efficiency decreases as the size of the data structure grows, making it less ideal for large datasets.

This table summarizes the main strengths and weaknesses of linear search:

Also Read: Sorting in Data Structure: Categories & Types [With Examples]

Now that you understand its strengths and weaknesses, let’s assess your knowledge with a small quiz.

MCQs on Program for Linear Search in C

1. What is linear search?

a) Searching only in sorted arrays

b) Checking each element in sequence until a match is found

c) Dividing the array into halves

d) Searching in a binary format

2. What is the best-case time complexity of linear search in C?

a) O(1)

b) O(log n)

c) O(n)

d) O(n²)

3. In a linear search program, what condition is used to find the target element?

a) arr[i] != key

b) arr[i] == key

c) arr[i] > key

d) arr[i] <= key

4. What does a linear search function typically return when the element is not found?

a) 0

b) -1

c) Null

d) Exit

5. Which loop is commonly used in a linear search implementation?

a) while

b) do-while

c) for

d) goto

6. Which of the following makes a linear search efficient in real-world conditions?

a) If the element is always at the end

b) If array is sorted

c) If element is near the beginning

d) If recursion is used

7. Which part of the function makes it reusable?

a) Global variables

b) Hardcoded array

c) Passing array and key as parameters

d) Inline scanf calls

8. What is the worst-case time complexity of linear search in C?

a) O(1)

b) O(n)

c) O(log n)

d) O(n log n)

9. You write a linear search function:

int search(int arr[], int n, int key) {
  for(int i = 0; i < n; i++) {
    if(arr[i] == key) return i;
  }
}

What’s the issue here?

a) Missing return when not found

b) Loop runs incorrectly

c) Incorrect syntax

d) It’s binary search

10. A candidate uses linear search to find the minimum value. What’s the problem?

a) Linear search is only for sorted arrays

b) It can’t return position

c) Linear search is for searching, not comparing values

d) Logic needs min tracking, not equality checking

11. You need to search for multiple occurrences of a number using linear search. What must be modified?

a) Exit loop after first match

b) Add return before loop

c) Remove return and store all indices in array

d) Use goto for efficiency

How Can upGrad Help You Master Linear Search in C?

upGrad’s courses provide hands-on training in C programming and algorithm design, covering searching techniques, loops, and data structures. Master linear search, optimize its efficiency, and build a strong foundation for software development and competitive coding.

Explore upGrad’s courses to elevate your programming skills and become proficient in search algorithms:

• Data Structures & Algorithms
• Advanced SQL: Functions and Formulas
• Learn Basic Python Programming
• JavaScript Basics from Scratch
• AI-Powered Full Stack Development Course by IIITB

You can also get personalized career counseling with upGrad to guide your career path, or visit your nearest upGrad center and start hands-on training today!

Similar Reads:

Explore C Tutorials: From Beginner Concepts to Advanced Techniques

C Compiler for Windows

String Anagram Program in C

C Program to check Armstrong Number

C Operators Tutorial : An Overview with Types and Examples

Array in C: Introduction, Declaration, Initialisation and More

Exploring Array of Pointers in C: A Beginner's Guide

Explain the array of structures in C language

C Program to Find ASCII Value of a Character

Discovering C Operators: An Overview with Types and Examples!

Binary Search in C

Dynamic Memory Allocation in C using malloc(), calloc(), free() and realloc()

C Enum Type: Definition and Practical Implementation

Evaluation of Arithmetic Expression: An Ultimate Guide

Factorial Program of a Number in C

15 Most Important Features of C Language

FAQs

1. How does linear search compare to binary search in terms of performance?

Linear search has O(n) time complexity, meaning it checks each element one by one, while binary search has O(log n) time complexity, making it more efficient for sorted arrays.

2. How does the linear search algorithm work with linked lists?

Linear search can be applied to linked lists by starting from the head node and traversing each node one by one, similar to arrays, until the target element is found.

3. Why is linear search inefficient for large datasets?

For large datasets, linear search requires checking each element sequentially, resulting in a significant number of comparisons, making it slower than algorithms that take advantage of sorted data or indexing.

4. Can linear search be implemented recursively?

Yes, linear search can be implemented recursively by checking the first element and then recursively calling the function on the rest of the array or list.

5. Does linear search stop once the target element is found?

Linear search stops immediately once the target element is found, making it an early termination algorithm. However, if it is not optimized, it still checks the remaining elements in its basic form.

6. What happens when the target element is absent in the array during linear search?

If the target element is absent, the algorithm will check all elements and return a value indicating that the element was not found (usually -1).

7. Why does linear search have a space complexity of O(1)?

Linear search uses a fixed amount of space, regardless of the input size, as it only requires a few variables for looping and comparisons, hence the space complexity remains O(1).

8. How do we optimize linear search for early termination?

Linear search can be optimized by stopping as soon as the target element is found and returning the index, avoiding unnecessary comparisons for the remaining elements.

9. Can linear search be applied to multi-dimensional arrays?

Yes, linear search can be applied to multi-dimensional arrays by treating them as a flattened one-dimensional array or by using nested loops to traverse each element.

10. What are the limitations of linear search in a real-world application?

Linear search is not suitable for applications requiring fast data retrieval from large datasets or sorted data, such as databases or search engines, where faster algorithms are preferred.

11. How does linear search handle duplicates in the array?

In the case of duplicates, linear search will return the index of the first occurrence of the target element and does not continue checking for subsequent matches unless modified.

Take a Free C Programming Quiz

Answer quick questions and assess your C programming knowledge

Start Quiz