If you have ever been into statistics, chances are you have read about the great debate— Bayesian vs. Frequentists. Each of these is merely an approach to solving a statistical problem related to probabilities. Now, Bayesian statisticians blame Frequentists for their methods and vice-versa. There is no end to this debate. Both have their advantages and disadvantages.
Best Machine Learning and AI Courses Online
In this article, we will look into both of the approaches and find out which one among the two is good for you for your next statistical problem.
Bayesians vs. Frequentists— In Terms of Probability Definition
Definition 1: Probability as a Degree of Belief by Frank Ramsey (Bayesian Approach)
Probability of an event is measured by the subjective degree of belief. It is also called the ‘Logical Probability’. This means your definition of probability might vary from someone else’s, if he/she has more evidence than you. This is completely fine and the other person can think whatever he wants to.
In-demand Machine Learning Skills
Get Machine Learning Certification from the World’s top Universities. Earn Masters, Executive PGP, or Advanced Certificate Programs to fast-track your career.
Definition 2: Probability as a Long-Term Frequency by Ronald Fisher (Frequentists Approach)
Probability of an event is equal to the long-term frequency of that event when it is repeated several times over and over. There is one universal answer and unlike definition 1, opinions to a probability of an event can not vary from person to person even if they have more/less evidence.
Example:
Suppose I have an unbiased normal coin having heads on one side and tails on the other. Now I toss the coin. I have the results. But, you as a spectator do not know if the coin is heads-up or tails-up.
So I want you to answer – “What is the probability that the coin I tossed is heads-up?”
There will be two different kinds of answers based on the two different definitions of probability.
Bayesians
Bayesians will answer that there is a 50% chance that the coin is heads-up. You as a Bayesian will say to me, “The answer is 50% heads-up for me. But yeah, you know the outcome of the tossing. So, you have a 100% probability that the coin is either heads or tails. But, you know what, I do not care. Because, as per the resources available to me, the answer is 50% for me.”
Frequentists
Frequentists will answer the question “There is either 100% chance or a 0% chance that the coin is heads-up. Since the coin has been landed, there is no use in attaching a probability to this fixed and constant value. The outcome of the tossing is final and there is no alteration to it. There will be no variation of answer among anyone.
Read: Types of Supervised Learning
Bayesian vs. Frequentists— In Terms of Use of Prior Probabilities
Let us look into another example.
We will take the above example a step further. I will toss the coin many times, suppose 14 times. You have noted down the results of the past 14 coin tosses. Now for the 15th time, I toss the coin again. Now, you are asked, “What is the probability that this tossed coin is heads up”.
Bayesians
If you are Bayesian, what you will use, is a term known as prior. Let us look into Bayes’ formula for conditional probability:
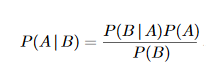
where A and B are some events and P(A | B) is defined as Probability of event A given event B has happened.
Now, the term P(A) is defined as prior which is defined as the probability that event A is true before the data is considered.
Coming back to the example, as a Bayesian, you will utilise the term prior i.e., you will make a decision based on the past results of coin tossings.
Suppose out of 14 coin tossings, I got heads-up 9 times. You might say that “Well, I have higher chances of getting a head”. Not only you say that, but your calculation will also support your argument. So your decision has been altered due to the ‘prior’ results. One’s ability to make decisions depends on one’s degree of belief in the chosen prior. Assigning prior probabilities has been one of the key factors in Bayesian’s results.
Must Read: Types of Regression Models in Machine Learning
Frequentists
If you are a Frequentist, you will completely disagree with whatever Bayesians say. You do not have any interest in the prior as the prior is often a guessed value. Rather your idea is based on the maximum likelihood estimate. What you will do is, you will collect sample data from a population. Now estimate the mean value which is mostly uniform with the mean of data. This value is the maximum likelihood point (estimate) of the uncertain parameter.
Now, Frequentists might assume that the sample mean would be equal to the population mean, which could be wrong and is indeed wrong most of the time. So they have introduced terms such as p-values and confidence intervals.
P-value is a simple way to measure the probability of finding observed or extreme results when the null hypothesis is true. You reject the null hypothesis when the p-value is below the level of significance of 0.05. Now, p-values and confidence intervals are important enough to dedicate a separate article for them.
So now as a first step, you collect the sample from the population. You repeat the procedure a large number of times. Now, your true mean should be within the confidence intervals you choose, having a certain probability. This is what you have to do to get the result for my coin-tossing question.
You may be thinking Frequentists are way too complex. Well, they are in a sense. They tend to find the perfect universal answer that can be accepted by anyone, despite various conditions. And by doing so, Frequentists do involve serious calculations and complexity which beginners might not understand.
Popular AI and ML Blogs & Free Courses
Conclusion
Bayesian vs. Frequentist— which is the way?
Bayesian vs. Frequentist debate will go on. But it is upon you, based on the resources available, which approach to use. Both approaches have their huge number of applications. The great Mathematician Laplace calculated the mass of Saturn using Bayesian inference which could have been very much tougher with Frequentist way.
On the other hand, the Frequentist way of thinking has helped recent researchers in solving problems efficiently especially in the field of medical science that could not have been done with Bayesian inference.
If you’re interested to learn more about machine learning, check out IIIT-B & upGrad’s PG Diploma in Machine Learning & AI which is designed for working professionals and offers 450+ hours of rigorous training, 30+ case studies & assignments, IIIT-B Alumni status, 5+ practical hands-on capstone projects & job assistance with top firms.









![Artificial Intelligence Salary in India [For Beginners & Experienced] in 2024](/__khugblog-next/image/?url=https%3A%2F%2Fd14b9ctw0m6fid.cloudfront.net%2Fugblog%2Fwp-content%2Fuploads%2F2019%2F11%2F06-banner.png&w=3840&q=75)
![24 Exciting IoT Project Ideas & Topics For Beginners 2024 [Latest]](/__khugblog-next/image/?url=https%3A%2F%2Fd14b9ctw0m6fid.cloudfront.net%2Fugblog%2Fwp-content%2Fuploads%2F2020%2F04%2F280.png&w=3840&q=75)
![Natural Language Processing (NLP) Projects & Topics For Beginners [2023]](/__khugblog-next/image/?url=https%3A%2F%2Fd14b9ctw0m6fid.cloudfront.net%2Fugblog%2Fwp-content%2Fuploads%2F2020%2F05%2F513.png&w=3840&q=75)
![45+ Interesting Machine Learning Project Ideas For Beginners [2024]](/__khugblog-next/image/?url=https%3A%2F%2Fd14b9ctw0m6fid.cloudfront.net%2Fugblog%2Fwp-content%2Fuploads%2F2019%2F07%2FBlog_FI_Machine_Learning_Project_Ideas.png&w=3840&q=75)